SFDやBMDの演習問題です。
大学の授業のテスト対策などにご活用ください。
以下の問の梁について、SFDおよびBMDを作成してください。
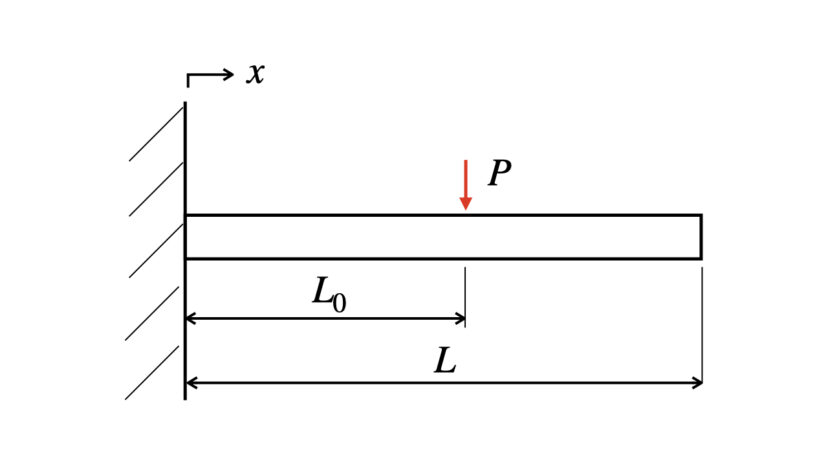
※Pは集中荷重とします。
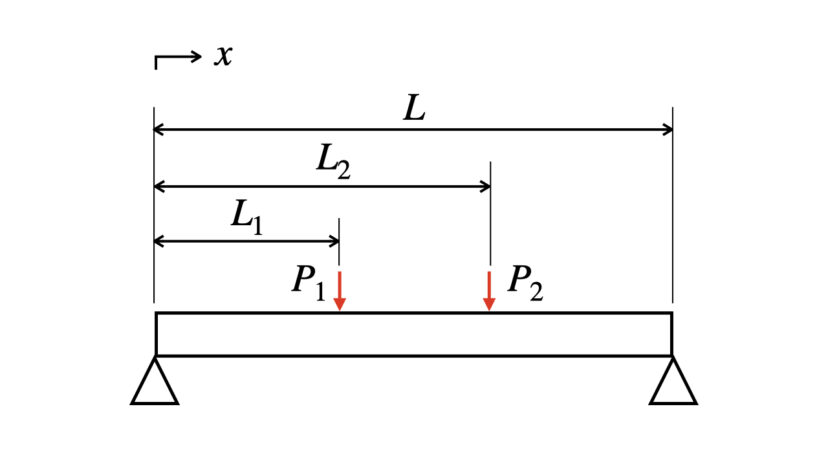
※P1、P2は集中荷重とします。
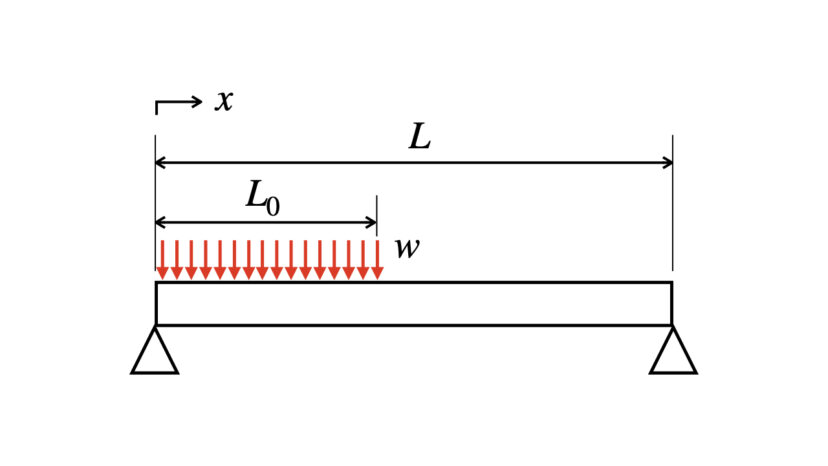
※wは分布荷重とします。
どの問題も基本的な流れは、
といった感じなります。
では、各問題に対しての解説に移ります。

上の図に反力を描き足すと、以下のようになります。
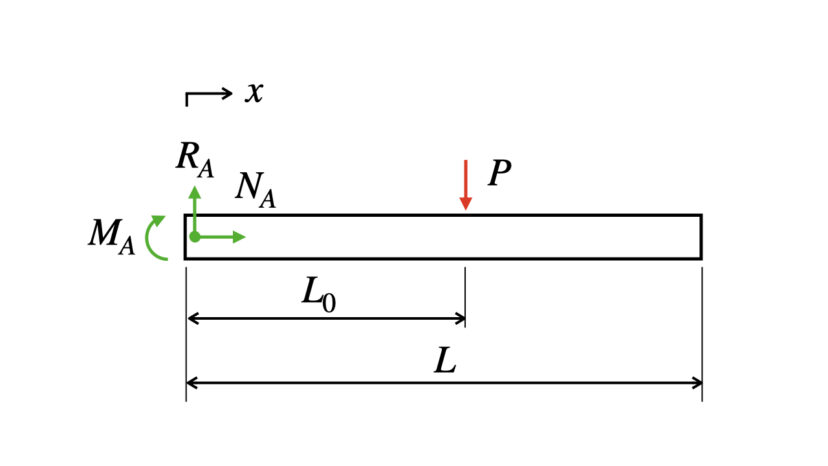
ではまず、釣り合いの式を立てます。
$$\begin{align}&(上下方向):R_A-P=0\cdots(1-1)\\&(左右方向):N_A=0\cdots(1-2)\\&(回転方向):M_A+L_0P=0\cdots(1-3)\end{align}$$
次に、梁を仮想的に切り離して考えてみるのですが、今回の場合、(0≦x≦L0)と、(L0≦x≦L)とで内力の値が変わります。
そのため、この2パターンで梁を仮想的に切り離して考えてみます。

問題によって、どこで仮想的に切り離せばよいかを判断できるようになるには「慣れ」が必要です。ただ、材料力学が得意な人は、計算をする前に頭の中に答えのイメージをすでに持っているという人が多いです。
ポイント
計算をする前に、荷重の場所の前後で、梁に発生する現象が変わることをイメージしておく
【ケース(a): 0≦x≦L0】
仮想的に切り離すと以下のようになります(左右方向には外力がかかっていないので、省略します)。
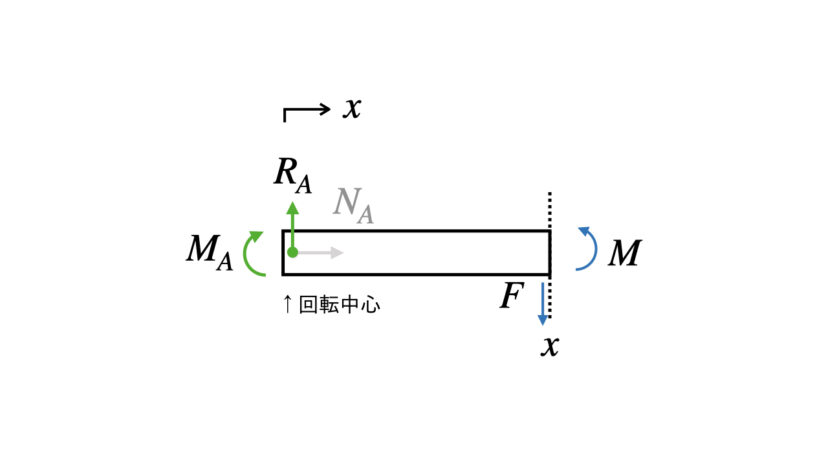
$$\begin{align}&(上下):R_A-F=0\cdots(1-4)\\&(回転):M_A+F\cdot x-M=0\cdots(1-5)\end{align}$$
では、計算していきます。(1-1)式と(1-4)式より、
$$\begin{align}\begin{cases}R_A-P=0\cdots(1-1)\\R_A-F=0\cdots(1-4)\\\end{cases}\end{align}$$
これを解くと、以下の通りになります。
$$\begin{align}&R_A=P\\&F=P\cdots(1-6)\end{align}$$
続いて(1-3)式、(1-5)式、(1-6)式より、
$$\begin{align}\begin{cases}M_A+L_0P=0\cdots(1-3)\\
M_A+F\cdot x-M=0\cdots(1-5)\\
F=P\cdots(1-6)\end{cases}\end{align}$$
これを解くと、以下のようになります。
$$\begin{align}&M_A=-L_0P\\&M=Fx-L_0P\cdots(1-7)\end{align}$$
これでケース(a)は完了です。
【ケース(b): L0≦x≦L】
仮想的に切り離すと以下の図のようになります。
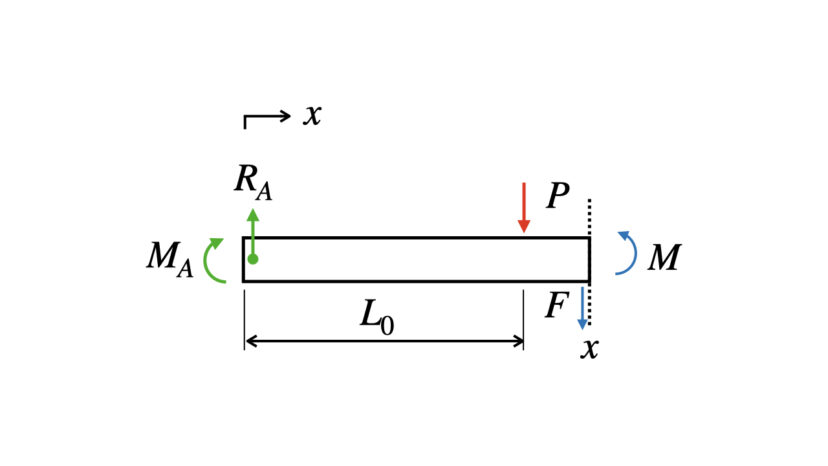
$$\begin{align}&(上下):R_A-P-F=0\cdots(1-8)\\
&(回転):M_A+L_0\cdot P+F\cdot x-M=0\cdots(1-9)\end{align}$$
(1-1)式と(1-8)式より、
$$\begin{cases}\begin{align}R_A-P=0\cdots(1-1)\\R_A–P-F=0\cdots(1-8)\end{align}\end{cases}$$
これを解くと、
$$F=0\cdots(1-10)$$
続いて、(1-3)式、(1-9)式、(1-10)式より、
$$\begin{cases}\begin{align}&M_A+L_0P=0\cdots(1-3)\\
&M_A+L_0\cdot P+F\cdot x-M=0\cdots(1-9)\\
&F=0\cdots(1-10)\end{align}\end{cases}$$
これを解くと、
$$M=0\cdots(1-11)$$
これでケース(b)は完了となります。
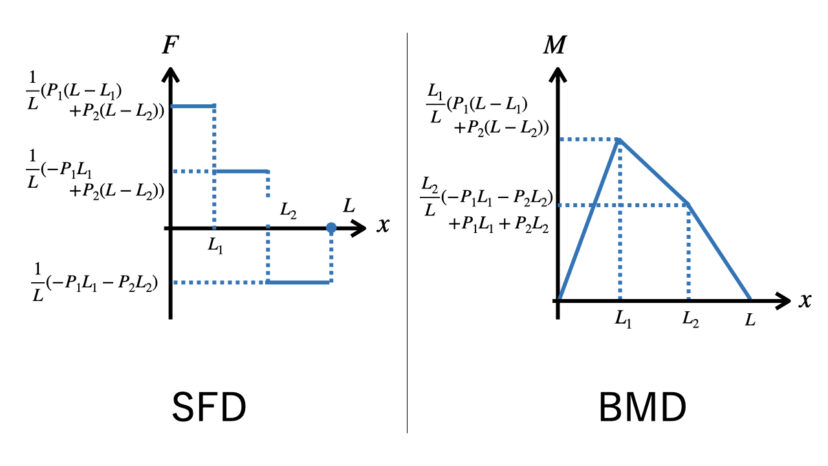
以上、SFDは(1-6)式と(1-10)式を合わせて、BMDは(1-7)式と(1-11)式を合わせて、以下の通りになります。
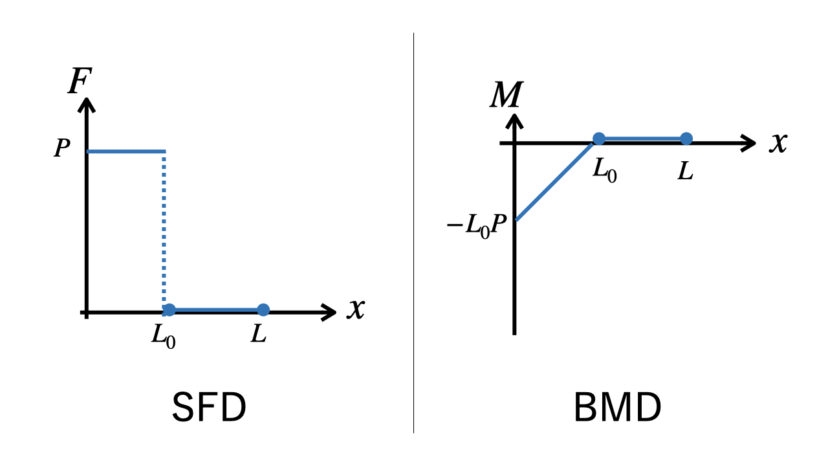

グラフについてですが、「直線なのか曲線なのか」「傾きや切片は正なのか負なのか」が合っていればOKですよー

一見複雑そうに見えても、やることは基本どおりで大丈夫です。
まずこの図に反力を描き足すと、次のようになります。
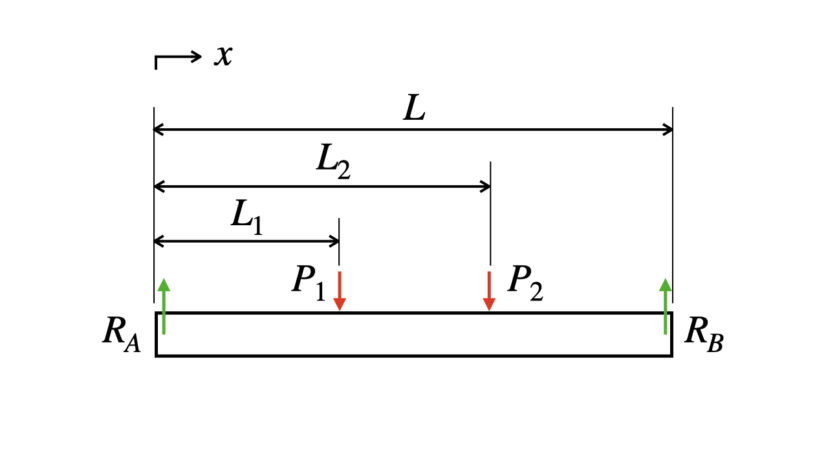

単純支持の場合、支持部はモーメントを受けることができないので、当然梁にかかるモーメントの反力も0になります。
よって、釣り合いの式は以下のとおりです。
$$\begin{cases}\begin{align}&(上下方向):R_A-P_1-P_2+R_B=0\\
&(回転方向):P_1L_1+P_2L_2-R_BL=0\\\end{align}\end{cases}$$
これを解くと、以下の通りとなります。
$$R_B=\frac{1}{L}\cdot(P_1L_1+P_2L_2)\cdots(2-1)\\
R_A=\frac{1}{L}\cdot(P_1(L-L_1)+P_2(L-L_2))\cdots(2-2)$$
では、続いて仮想的に切り離してみるのですが、今回は集中荷重が2箇所ありますので、場合分けは、
の3パターンになります。
あとは、各パターンについて淡々と計算し、最後にグラフを作成していきましょう。
【ケース(a); 0≦x≦L1】
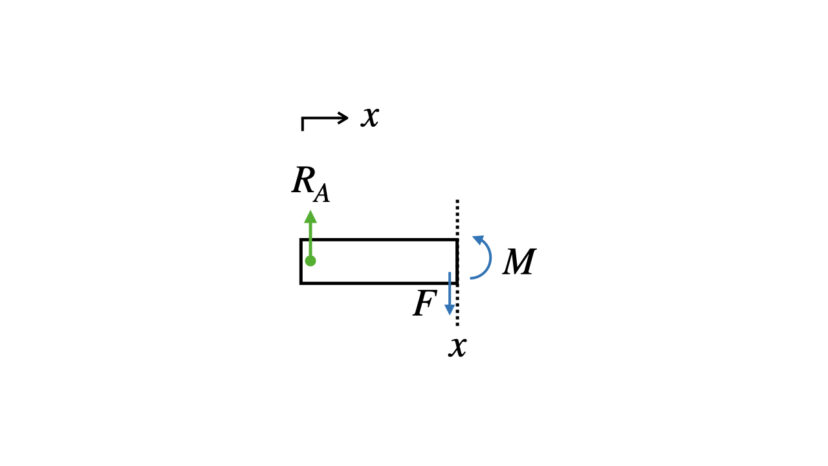
$$\begin{cases}\begin{align}&(上下方向):R_A-F=0\cdots(2-3)\\
&(回転方向):Fx-M=0\cdots(2-4)\end{align}\end{cases}$$
(2-2)式、(2-3)式、(2-4)式より
$$\begin{cases}\begin{align}&R_A=\frac{1}{L}\cdot(P_1(L-L_1)+P_2(L-L_2))\cdots(2-2)\\
&R_A-F=0\cdots(2-3)\\
&Fx-M=0\cdots(2-4)\end{align}\end{cases}$$
これを解くと、以下の通りとなります。
$$\\ F=\frac{1}{L}\cdot(P_1(L-L_1)+P_2(L-L_2))\cdots(2-5)\\
M=\frac{x}{L}\cdot(P_1(L-L_1)+P_2(L-L_2))\cdots(2-6)$$
これでケース(a)は完了となります。
【ケース(b): L1≦x≦L2】
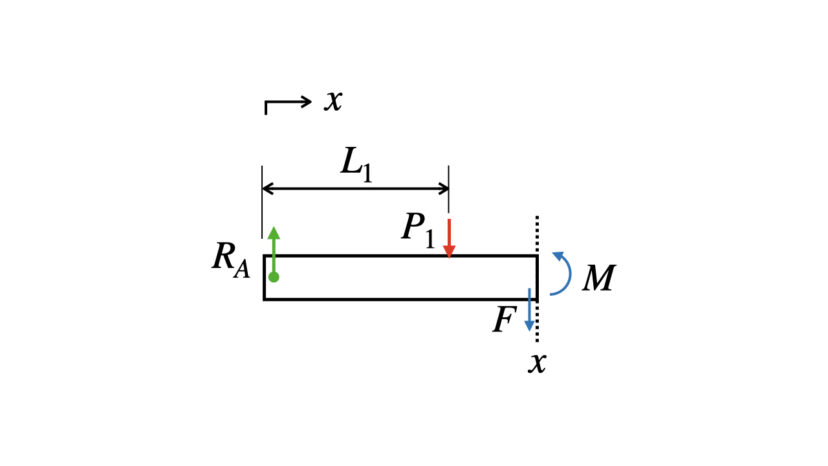
$$\begin{cases}\begin{align}&(上下方向):R_A-P_1-F=0\cdots(2-7)\\
&(回転方向):P_1L_1+Fx-M=0\cdots(2-8)\\\end{align}\end{cases}$$
(2-2)式、(2-7)式、(2-8)式より
$$\begin{cases}\begin{align}&R_A=\frac{1}{L}\cdot(P_1(L-L_1)+P_2(L-L_2))\cdots(2-2)\\
&R_A-P_1-F=0\cdots(2-7)\\
&P_1L_1+Fx-M=0\cdots(2-8)\\\end{align}\end{cases}$$
これを解くと、以下の通りとなります。
$$\\F=\frac{1}{L}\cdot(-P_1L_1+P_2(L-L_2))\cdots(2-9)\\
M=\frac{x}{L}\cdot(-P_1L_1+P_2(L-L_2))+P_1L_1\cdots(2-10)$$
これでケース(b)は完了となります。
【ケース(c): L2≦x≦L】
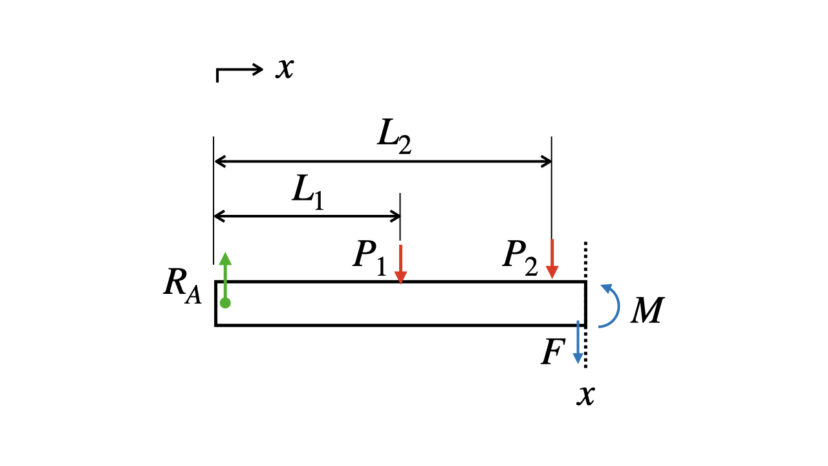
$$\begin{cases}\begin{align}&(上下方向):R_A-P_1-P_2-F=0\cdots(2-11)\\
&(回転方向):P_1L_1+P_2L_1+Fx-M=0\cdots(2-12)\end{align}\end{cases}$$
(2-2)式、(2-11)式、(2-12)式より
$$\begin{cases}\begin{align}&R_A=\frac{1}{L}\cdot(P_1(L-L_1)+P_2(L-L_2))\cdots(2-2)\\
&R_A-P_1-P_2-F=0\cdots(2-11)\\
&P_1L_1+P_2L_1+Fx-M=0\cdots(2-12)\\\end{align}\end{cases}$$
これを解くと、以下の通りとなります。
$$\\F=\frac{1}{L}(-P_1L_1-P_2L_2)\cdots(2-13)\\
M=\frac{x}{L}(-P_1L_1-P_2L_2)+P_1L_1+P_2L_2\cdots(2-14)$$
これでケース(c)は完了となります。
以上、SFDは(2-5)式と(2-9)式と(2-13)式を合わせて、BMDは(2-6)式と(2-10)式と(2-14)式を合わせて、以下の通りになります。
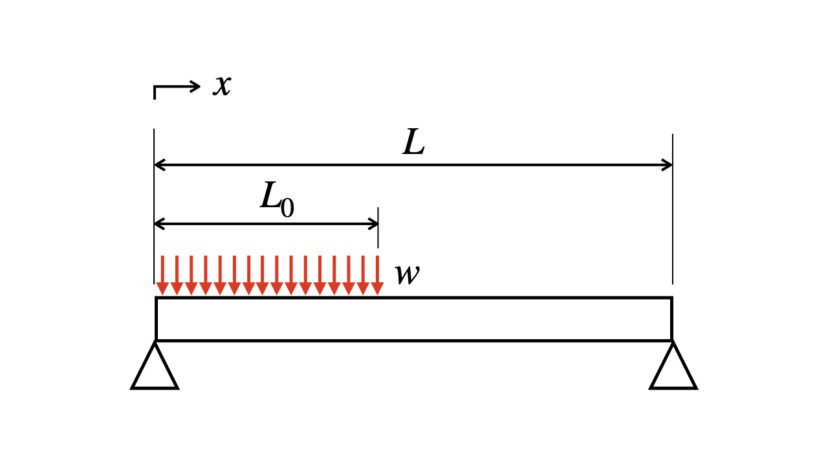
両端支持梁の等分布荷重の問題です。
まず荷重が「等分布荷重」であることから、これを集中荷重に置き換えます。
そして、反力も描き足すと、以下のとおりとなります。
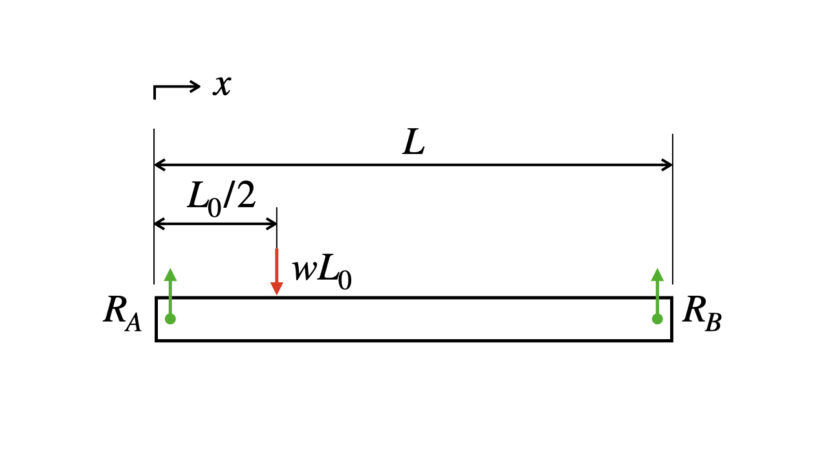
$$\begin{cases}\begin{align}&(上下方向):R_A-wL_0+R_B=0\\
&(回転方向):wL_0\frac{L_0}{2}-R_BL=0\\\end{align}\end{cases}$$
これを解くと、以下の通りとなります。
$$R_B=\frac{wL_0^2}{2L}\cdots(3-1)
\\R_A=wL_0\cdot(1-\frac{L_0}{2L})\cdots(3-2)$$
では、仮想的に切り離すのですが、今回は
の2パターンで場合分けをします。
【ケース(a):0≦x≦L0】
まずケース(a)の解説をする前に、よくやらかしてしまいがちな注意点を言っておきます。
最初に「等分布荷重を集中荷重に変換する」ということをやったかと思いますが、仮想的に切り離す前にいったん等分布荷重へ戻してください。
そして、仮想的に切り離した後、もう一度集中荷重へ変換します。
ポイント
仮想的に切り離す前に、いったん等分布荷重へ戻す。仮想的に切葉した後に、改めて集中荷重へ置き換える。
このような操作をする理由は以下の切り離しの図を見てもらえるとわかるかと思いますが、仮想的に切り離す前と後とで、梁に作用する荷重が変わるからです。
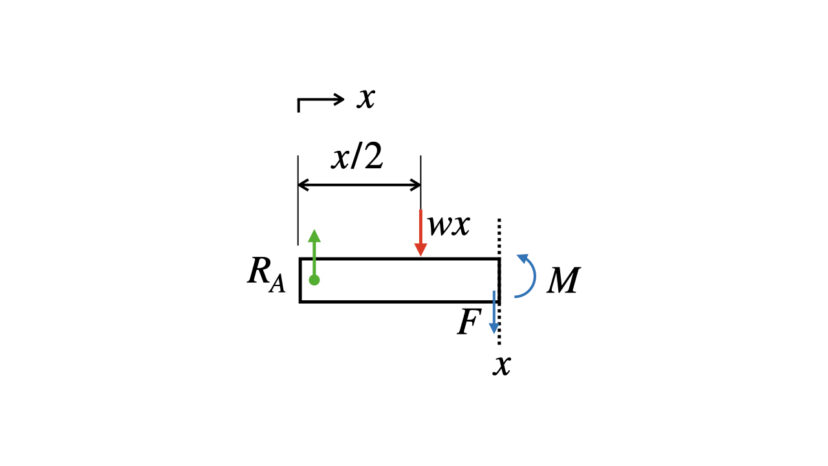
$$\begin{cases}\begin{align}
&(上下方向):R_A-wx-F=0\cdots(3-3)\\
&(回転方向):wx\frac{x}{2}+Fx-M=0\cdots(3-4)
\end{align}\end{cases}$$
(3-2)式、(3-3)式、(3-4)式より、
$$\begin{cases}\begin{align}
R_A=wL_0\cdot(1-\frac{L_0}{2L})\cdots(3-2)\\
R_A-wx-F=0\cdots(3-3)\\
wx\frac{x}{2}+Fx-M=0\cdots(3-4)
\end{align}\end{cases}$$
これを解くと、以下の通りとなります。
$$F=wL_0(1-\frac{x}{L_0}-\frac{L_0}{2L})\cdots(3-5)\\
M=-\frac{wx^2}{2}+wL_0(1-\frac{L_0}{2L})x\cdots(3-6)$$
これで、ケース(a)は完了となります。
【ケース(b):L0≦x≦L】
続いてケース(b)ですが、こちらも切り離す前に一度分布荷重へ戻しましょう。
ポイント
仮想的に切り離す前に、いったん等分布荷重へ戻す。仮想的に切葉した後に、改めて集中荷重へ置き換える。
切り離し後に改めて集中荷重に変換し、図に反映させると以下の通りとなります。
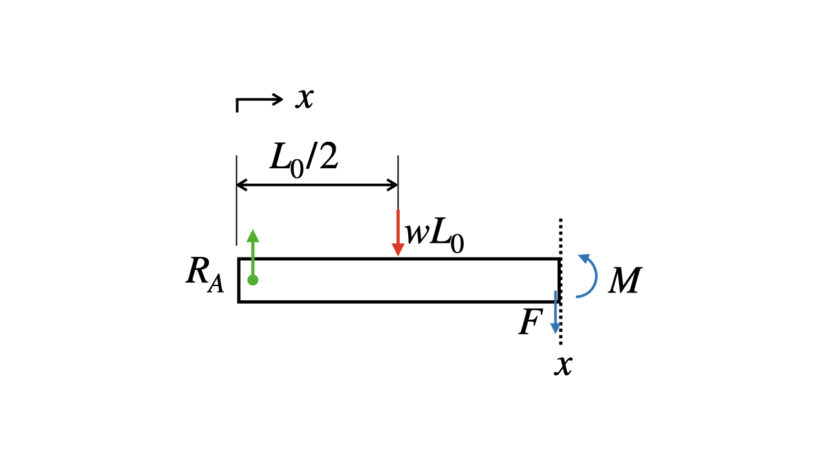
$$\begin{cases}\begin{align}
&(上下方向):R_A-wL_0-F=0\cdots(3-7)\\
&(回転方向):wL_0\frac{L_0}{2}+Fx-M=0\cdots(3-8)
\end{align}\end{cases}$$
(3-2)式、(3-7)式、(3-8)式より
$$\begin{cases}\begin{align}
&R_A=wL_0\cdot(1-\frac{L_0}{2L})\cdots(3-2)\\
&R_A-wL_0-F=0\cdots(3-7)\\
&wL_0\frac{L_0}{2}+Fx-M=0\cdots(3-8)
\end{align}\end{cases}$$
これらについて解くと、以下の通りとなります。
$$F=-\frac{wL_0^2}{2L}\cdots(3-9)
\\M=\frac{wL_0^2}{2}(1-\frac{x}{L})\cdots(3-10)$$
これでケース(b)は完了となります。
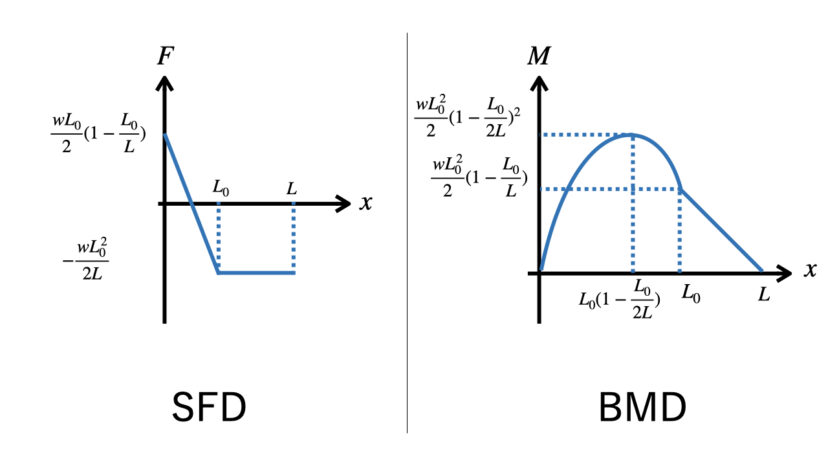
以上、SFDは(3-5)式と(3-9)式とを合わせて、BMDは(3-6)式と(3-10)式を合わせて、以下の通りになります。
【補足:BMDの最大値の求め方】
問3で最後の難関になっているのは、BMDの最大値と、その時のxの値の求め方だと思います。
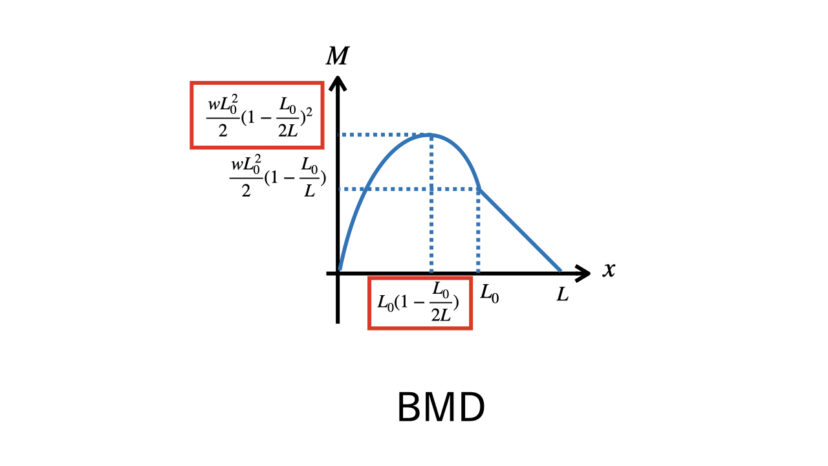
これについて解説していきます。
主な求め方は2通りあり、「(1)xについて微分をし、その時のxの値を求める。その後、そのxのときのモーメントを求める」「(2)平方完成をし、2次関数の頂点の座標を求める」
お好きな方でよいのですが、それぞれ解説してきます。
【(1)の求め方】
(3-6)式の右辺をf(x)とおき、これを微分します。
$$f'(x)=-wx+wL_0(1-\frac{L_0}{2L})$$
よって、f'(x)=0となるようなxの値は、
$$-wx+wL_0(1-\frac{L_0}{2L})=0$$
$$x=L_0(1-\frac{L_0}{2L})=0$$
これを(3-6)式に代入すれば、
$$\begin{align}M&=-\frac{w}{2}\left(L_0(1-\frac{L_0}{2L})\right)^2+wL_0(1-\frac{L_0}{2L})(L_0(1-\frac{L_0}{2L}))\\
&=\frac{wL_0^2}{2}\left(1-\frac{L_0}{2L}\right)^2\end{align}$$
【(2)の求め方】
二次関数の頂点の座標を求めたいので、(3-6)式を以下の形にすることを目指します。
$$M=a(x-x_1)^2+y_1$$
この形にできた時、座標(x1, y1)が頂点の座標となります。
これを(3-6)式に当てはめると、
$$\begin{align}M &=-\frac{wx^2}{2}+wL_0(1-\frac{L_0}{2L})x\cdots(3-6)\\
&=-\frac{w}{2}\left(x-L_0(1-\frac{L_0}{2L})\right)^2+\frac{wL_0^2}{2}\left(1-\frac{L_0}{2L}\right)^2\end{align}$$
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

【解説】曲げ応力とは、どんな応力か?
曲げ応力の考え方の土台は、中立軸