今回は、曲げ応力の求め方について、お話を進めていきます。
曲げ応力は、梁の中立軸、および中立面を土台にして考えていきます。
この土台から、曲げ応力へどのように展開をしていくのか?
それは「材料の変形量」に注目をして、お話をしていきます。
この変形量から求めていく方法は、引張の不静定問題や、熱応力でもやったようなやり方ですね。
なおここでは、問題を簡略化することで、可能な限りわかりやすく説明している反面、厳密性が低くなりますことをご了承ください。
それでは、曲げ応力の求め方について、少しずつ話を進めていきます。
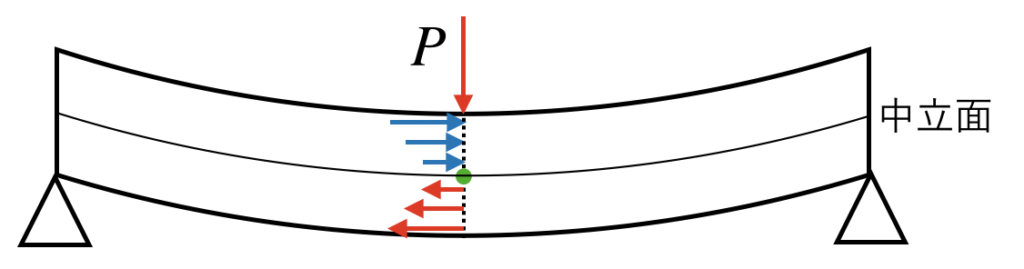
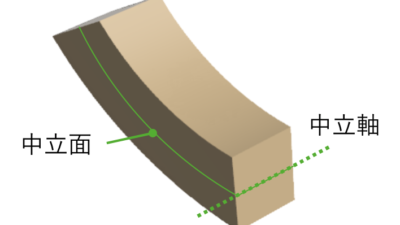
中立面とは、材料に発生する内力が0の面のことです。
ここで、材料力学の基本的な考え方を思い出してください。
材料は塑性変形をしない限り、荷重を受ければ変形します。
裏を返せば、材料は荷重を受けていなければ、変形しません。
この原理を利用します。
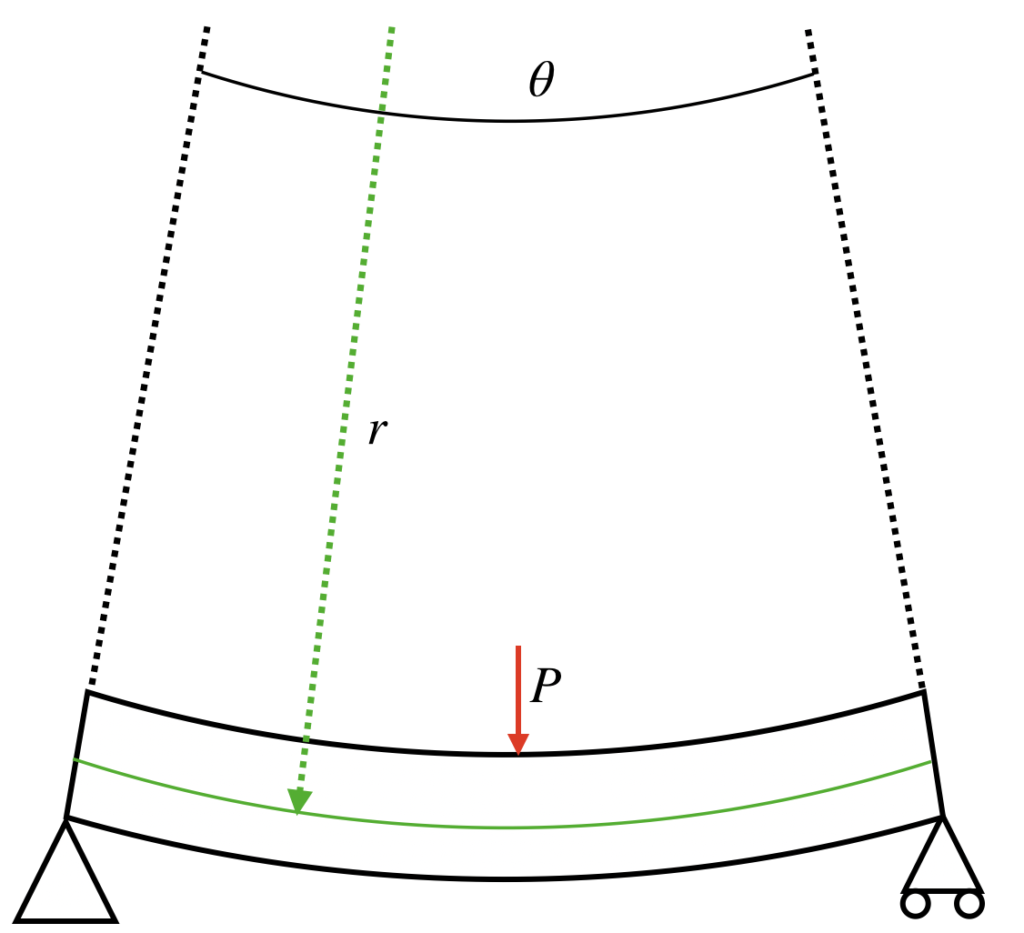
例えば、以下のような長さがLの両端支持梁について考えます(片側が移動支持のため、軸力は考慮しません)。
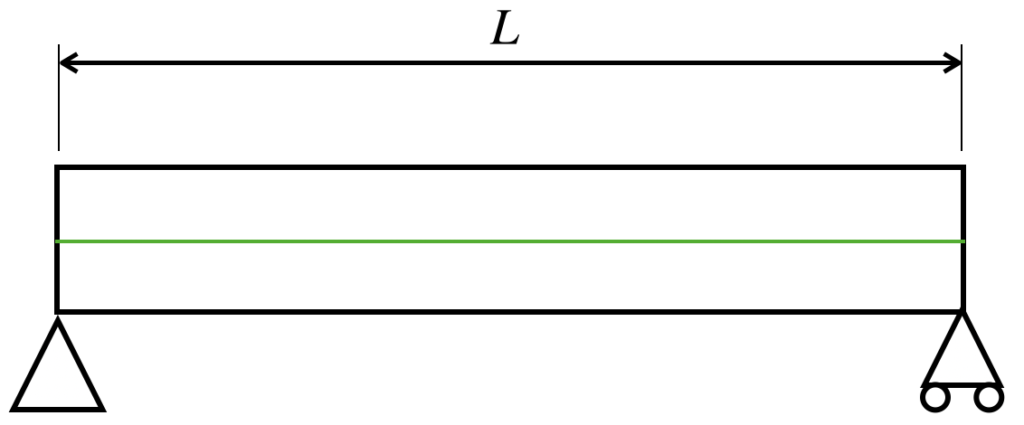
この梁の中央に集中荷重を与えます。

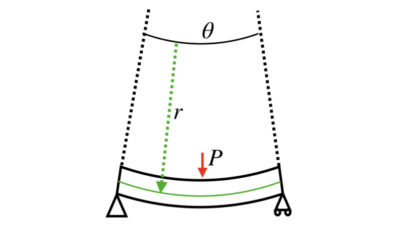
ではまず、緑色の線の長さを求めてみましょう。
まず、変形前の梁の長さより、緑の線の長さはLです。
次に変形後の梁に着目します。
ここで、この変形した梁は、円弧状に変形するという仮定をします。
すると、緑色の円弧は、その半径rと、角度θの掛け算で表現することができます(ここでいう角度はラジアンです)。
ちなみに、中立面はその定義の通り、変形量、およびひずみは0です。
[mathjax]
$$L=r\theta\cdots(1)
$$
では次に、この中立面から少し離れたところの変形量・びずみについて注目します。
中立面に垂直な座標軸をy軸とし、中立面の位置をy=0とします。
そして、そこからyだけ離れた赤い線の長さを求めてみます。
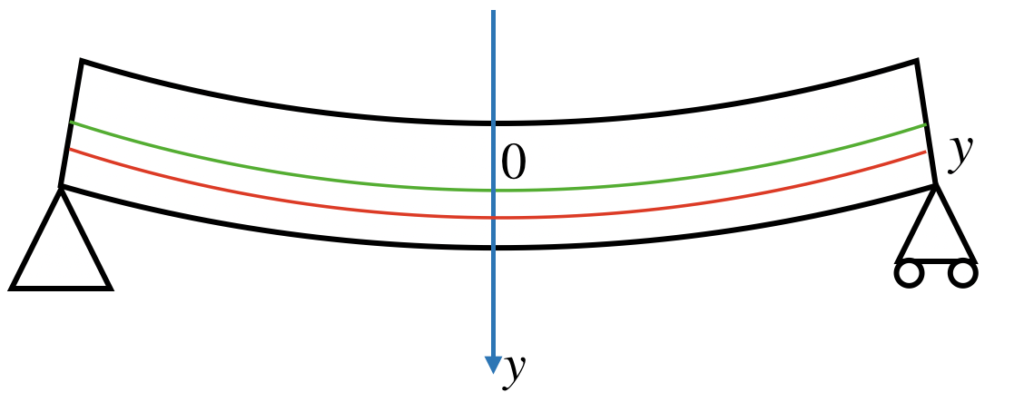
赤い線もまた円弧であるため、半径×角度で求めることができます。
半径はrからyだけ離れているので「r+y」
角度は中立面と同じで「θ」ですので、
$$(r+y)\theta$$
となります。
ところで、赤い線は中立面ではありませんので、変形・ひずみが発生します。
ひずみは、(「変形後の長さ」–「元の長さ」)/「元の長さ」で求まりますから、(1)式と合わせて、
$$\begin{align}
\varepsilon&=\frac{(r+y)\theta-r\theta}{r\theta}\\
&=\frac{y}{r}
\end{align}$$
となります。
ここで、このひずみは「垂直ひずみ」ですから、フックの法則が成り立ちます。
$$\begin{align}
\sigma=E\varepsilon=E\frac{y}{r}\cdots(2)
\end{align}$$
となります。
Eやrは一定の値であるため、
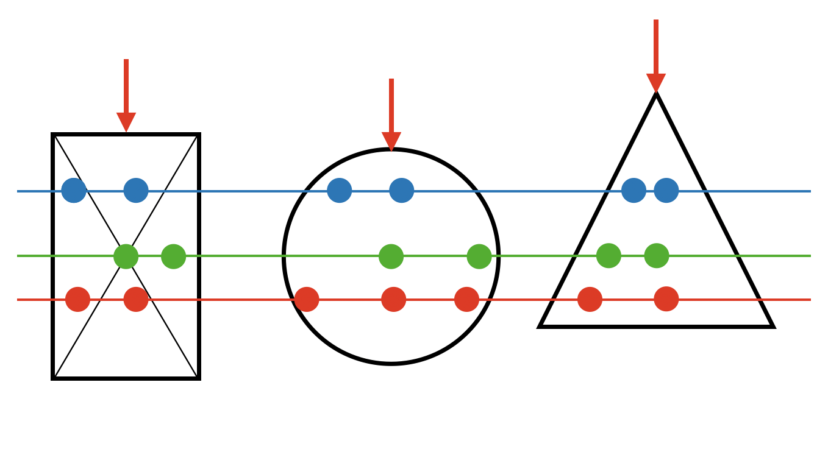
材料に発生する応力の大きさは、中立面からの距離に依存するという意味になります。
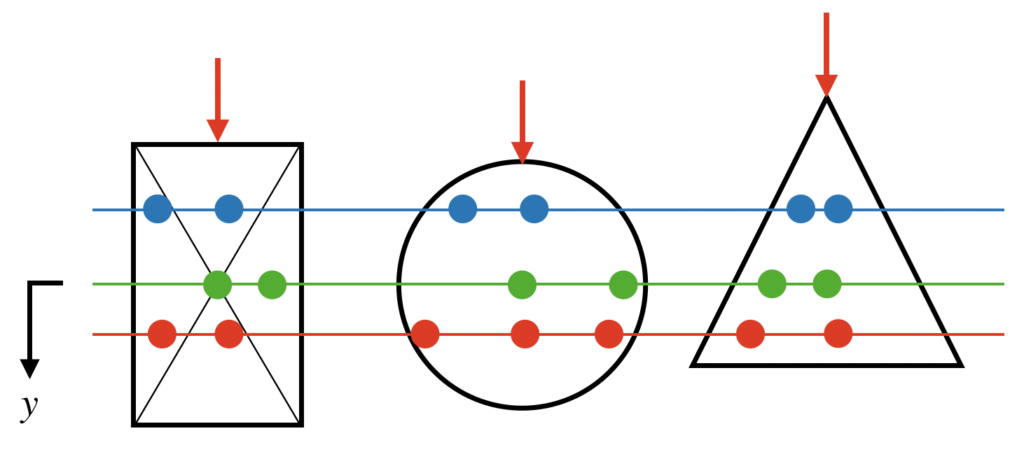
下の図は、さまざまな梁の断面形状を表していますが、同じ色の場所ならどこの点でも応力は同じです。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

曲げ応力の考え方の土台は、中立軸
曲げモーメントから読み解く、梁の曲率半径の導出