こんにちは!リヴィです。
今回は、締付けトルクと軸力の関係式の導出についての第4回目です。
前回までで、締付けトルクと軸力の関係式について解説いたしました。
その式は、以下の通りとなるとのことでした。
$$T=T_s+T_w=F_a \left (\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)$$
| $$T$$ | 締付けトルク |
| $$T_s$$ | ねじ面で必要な締付けトルク |
| $$T_w$$ | 座面で必要な締付けトルク |
| $$F_a$$ | 軸力 |
| $$P$$ | ねじ山のピッチ |
| $$d_2$$ | ねじの有効径 |
| $$\mu_s$$ | 摩擦係数 |
| $$\alpha$$ | ねじ軸に沿った断面で切ったときの、ねじ山の半角 |
| $$\mu_w$$ | 座面と母材との滑り摩擦係数 |
| $$d_w$$ | 等価摩擦直径 |
主な式の導出については前回までで完了ですが、今回はこの式に関係するその他の知識・注意点について解説いたします。
締付けトルクと軸力の関係式の使い方は、「発生させる軸力を決めて、それに必要な締付けトルクを、式を使って計算する」というものでした。
ですが、それ以外にも「ボルトをさらに締め込んだり、逆に緩めるのに必要なトルクを計算する」のにも使えます。
まず、ある軸力がすでに発生しており、その状態からさらにねじを締め込むのに必要な締付けトルクについて考えてみましょう。
考えるべき図は、前回までに解説した「締付けトルクと軸の関係式」で使われた図と同じになります。
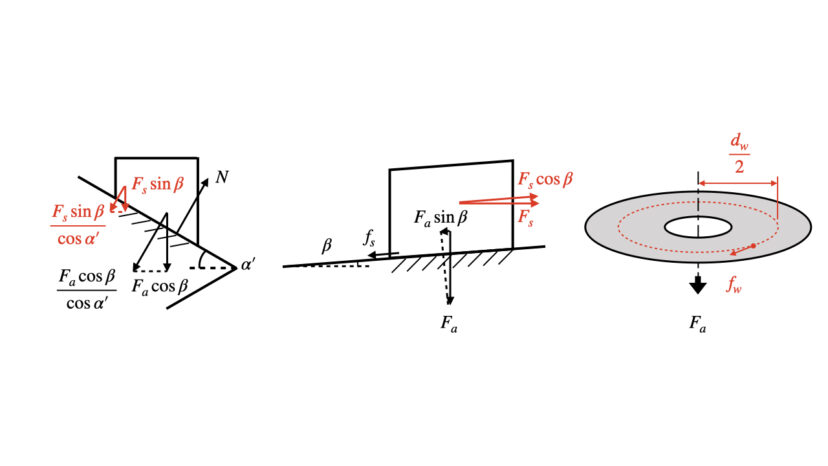
よって、ねじを更に締め付けるための条件は以下の通りとなります。
$$T>F_a \left (\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)\cdots(1-1)$$
一方で、ねじを緩めるのに必要な力となると、接線力のベクトルが逆となり、以下の通りとなります。
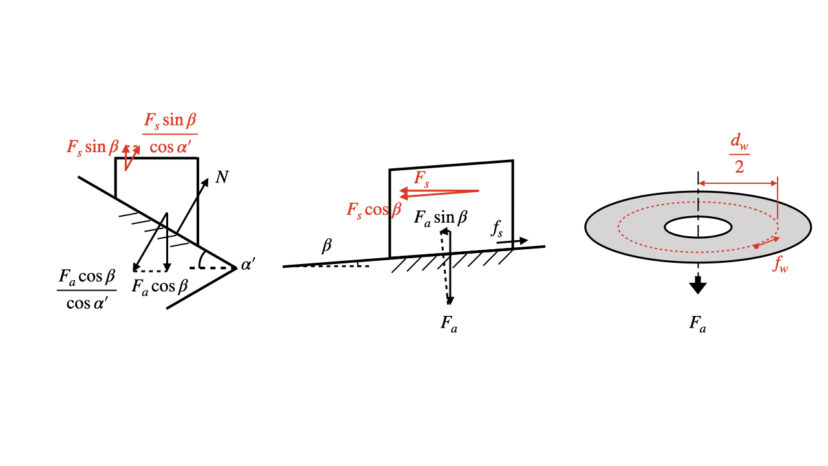
よって、ねじを緩めるための条件は以下の通りとなります。
$$T>F_a \left (-\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)\cdots(1-2)$$
そのため、締め付けるために必要な締付けトルクに比べ、緩めるのに必要な締付けトルクの方が小さくなるのです。

トルクレンチでトルクを測定するときには、必ず締める方向に回して測定する必要があります。「ボルトを締めすぎたから、緩めながら測定」したり、「ボルトが緩んだ瞬間の締付けトルク=ボルト締結時の締付けトルク」としたりする人がいますが、それは間違いです。
ねじを締め付ける際にかけたトルクのうちのほとんどは、摩擦力に打ち勝つために必要となります。
(1-1)式の、ねじを締め付ける条件式を見てみましょう。
$$T>F_a \left (\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)\cdots(1-1)$$
この式の右辺について、各項の大きさを見積ってみましょう。
| 項 | 説明 | 全体に占めるおおよその割合 |
|---|---|---|
| $$\frac{P}{2\pi}$$ | 軸力に起因する緩み方向の力 | 10% |
| $$\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}$$ | ねじ面の摩擦力 | 40% |
| $$\mu_w \frac{d_w}{2}$$ | 座面の摩擦力 | 50% |
上の表を見て分かる通り、私たちが一生懸命ねじを締めるときにかけた力のほとんどは、摩擦力に打ち勝つために使われるのです。

もちろん、ねじを緩めるのに必要な力についても同様のことが言えます。そのため、ねじが緩まないのはこの摩擦力のおかげが大きいということも言えるのです。
軸力と締付けトルクの関係式には摩擦係数が含まれていおりますが、それが静摩擦係数なのか、動摩擦係数なのかによって、必要な締付けトルクは異なってきます。
当然、静摩擦係数は、動摩擦係数よりも大きくなります。
そのため、トルクレンチでトルクを測定する際には、注意しなければなりません。
例えば、軸力を決めて、それに相当する締め付けトルクを「静摩擦係数」で計算したにもかかわらず、
トルクレンチを勢いよく回しながら測定すると、ねじを締めすぎてしまう恐れがあるのです。

かと言って、ねじ面が動かないとねじを締めることができません。そのため、トルクレンチ測定は、「ちょっと回したら除荷する」というのを繰り返しながら行う必要があるのです。
第2回のねじ面の力関係の解説で四角ねじが登場しましたが、「一般的に固定用ねじに使われるねじ山は、四角ではなくなぜ三角形なのか?」について解説していきます。
ここで、(1-2)式のねじを緩めるための条件式を以下に示します。
$$T>F_a \left (-\frac{P}{2\pi}+\frac{d_2}{2}\frac{\mu_s}{\cos\alpha}+\mu_w \frac{d_w}{2} \right)\cdots(1-2)$$
この式を使って、四角ねじの場合と、三角ねじの場合とでねじ緩めるために必要な力を比較していきます。
まず四角ねじについてですが、四角ねじのねじ山の半角は0°とみなすことができます。
よって、cosαは1になることから、(1-2)式は以下の通りとなります。
$$T>F_a \left (-\frac{P}{2\pi}+\frac{d_2}{2}\mu_s+\mu_w \frac{d_w}{2} \right)\cdots(2-1)$$
一方で三角ねじについて、ねじ山の半角は30°であることから、cosαは√3/2となります。
よって、(1-2)式に適用させると以下の通りとなります。
$$T>F_a \left (-\frac{P}{2\pi}+\frac{d_2}{2}\frac{2\mu_s}{\sqrt{3}}+\mu_w \frac{d_w}{2} \right)\cdots(2-2)$$
(2-1)式と(2-2)式を比べると、(2-2)式の方が必要なトルクが大きい、つまり「三角ねじの方が緩みにくい」ということが言えるのです。
このことから、固定用ねじには三角ねじが多く使われているのです。
締付けトルクと軸力の関係式について、今まで散々複雑な式を扱ってきましたが、多くのねじの参考書・専門書では、この式はあまり使われません。
では、どのような式が使われるのかというと、より簡素化された以下の式を使います。
$$T=KF_ad\cdots(3-1)$$
| $$T$$ | 締付けトルク[N・m] |
| $$K$$ | トルク係数[-] |
| $$F_a$$ | 軸力[N] |
| $$D$$ | ねじの呼び径[mm] |
つまり、締付けトルクと軸力の関係式のごちゃごちゃした部分について、トルク係数Kという係数を導入することによって、シンプルに表現しているのです。
ちなみに、簡素化する前の式と比較すると、トルク係数Kは以下のようになります。
$$K=\frac{1}{2d} \left( \frac{P}{\pi}+d_2\frac{\mu_s}{\cos\alpha}+\mu_w d_w \right)\cdots(3-2)$$
え、そんなことやっていいものなの!?
そう思う人もいるかと思いますので、一つずつ解説していきます。
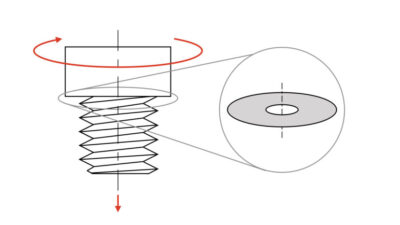
トルク係数の前にまず注目するべきなのは、(3-1)式のなかに「ねじの呼び径」が入っており、逆に「ねじの有効径」や「が入っていないことです。
これまで、「ねじに関する計算をする際は、ねじの有効径」を使うと説明してきたにも関わらず、なぜでしょうか?
これはあくまで私の推測ですが、実際ねじの計算で「ねじの有効径」を使おうとすると、いちいちねじの有効径を調べなければならず、とても手間なのです。
そのため、できるだけ「ねじの呼び径」で計算ができるようにすることで、計算しやすい式にしているのだと思われます。
なお、式(3-2)を見ると、分母に「ねじの呼び径」が入っていることから、ここでちゃんと打ち消し合うようになっています。
わざわざ係数とまとめたからには、その係数には何かしらの意味がありそうですが、一体トルク係数にはどんな意味があるのでしょうか。
結論から言うとトルク係数は、ボルトのねじ部や座面の摩擦係数に依存する係数という意味になります。
どういうことか、トルク係数Kの中身について詳しく見ていきましょう。
$$K=\frac{1}{2d} \left (\frac{P}{\pi}+d_2\frac{\mu_s}{\cos\alpha}+\mu_w d_w \right)\cdots(3-2)$$
| $$D$$ | ねじの呼び径 |
| $$P$$ | ねじ山のピッチ |
| $$d_2$$ | ねじの有効径 |
| $$\mu_s$$ | 摩擦係数 |
| $$\alpha$$ | ねじ軸に沿った断面で切ったときの、ねじ山の半角 |
| $$\mu_w$$ | 座面と母材との滑り摩擦係数 |
| $$D_w$$ | 等価摩擦直径 |
まずはP、D2、cosα、Dwの4つについてです。
これらの文字に共通すつ特徴は「ねじの種類・呼び径」が決まれば、ほぼ一意に決まるということです。
そのため、近似のやり方は資料によって異なるものの、「近似をしていくとだいたいこれぐらいの数字になるよ」という具体的な数字としてまとめられていることが多いです。
例えば、福岡俊道著, 技術者のためのねじの力学によると、トルク係数は以下のように近似されると述べられております。
$$(並目ねじ)\hspace{18pt}K=0.556\mu_s+0.65\mu_w+0.019\hspace{18pt}$$
$$(細目ねじ)\hspace{18pt}K=0.565\mu_s+0.65\mu_w+0.011\hspace{18pt}$$
あるいは、辻らの研究では、xという文字が使われ、近似的に以下ように定義されています。
$$x=\frac{d_2}{2d}\left(\frac{P}{\pi d_2}+1.155\mu_s\right)$$
一方で、μsやμwの値は、ねじの種類・呼び径」が決まったとしても、どういった数字になるか決定されることはありません。
これら摩擦係数は、
といった複雑な要素が絡むため、正確に特定することは不可能です。
とはいっても「全く特定できません」では使い物にはならないため、JIS B 1083では以下のように目安が示されております。
| μs,μw | K |
|---|---|
| 0.08 | 0.115 |
| 0.10 | 0.138 |
| 0.12 | 0.161 |
| 0.15 | 0.196 |
| 0.20 | 0.254 |
| 0.25 | 0.312 |
| 0.30 | 0.370 |
| 0.35 | 0.427 |
| 0.40 | 0.485 |
| 0.45 | 0.543 |
| μs,μw | K |
今回は、ねじの力関係について、その他の知識や注意点などについて解説をしていきました。
特にトルクレンチで測定する際には、ここで解説をしたようにいくつか注意しなければならないことがあります。
ねじのトラブルを発生させないためにも、ぜひ抑えておきたいポイントです。
ここまで、全4回に渡って盛りだくさんでねじの解説をしてきました。
なるべくわかりやすく説明をしたつもりですが、やはり1回見ただけでは分かりづらいところもあるかと思います。
わからないところについては、ぜひ何度も読み直していただければと思います。
それでは、ねじの力関係については以上となります。ご一読ありがとうございました。
ねじ関連のおすすめ書籍▼
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

【解説】締め付けトルクと軸力の関係式の導出(3)
【要注意】トルク法でボルトを締める際の、軸力のばらつきの大きさ