こんにちは!リヴィです。
今回は、締付けトルクと軸力の関係式の導出についての第3回目です。
第一回にて、必要となる締付けトルクは、以下の2つに分けて考えることができると説明をしました。
$$T=T_s+T_w$$
| $$T$$ | 締付けトルク |
| $$T_s$$ | ねじ面で必要な締付けトルク |
| $$T_w$$ | 座面で必要な締付けトルク |
このうち、今回は「座面で必要な締付けトルク」に着目して、解説をしていきます。
今回は締付けトルクのうち、座面で必要な締付けトルクについて解説していきます。

ねじ面の話と比べると、かなり簡単ですので、安心してください(笑)。
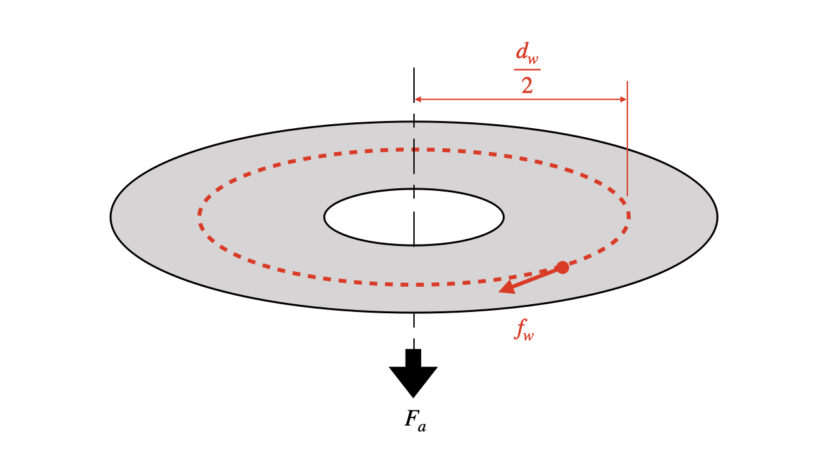
座面で発生する摩擦力については、各接触点ごとに摩擦力を計算するのではなく、「等価摩擦直径と呼ばれる位置にて座面の摩擦力が全て働く」と考えることで、シンプルになります。
等価摩擦直径とは、以下の式で表される直径のことを指します。
$$d_w=\frac{2}{3}\cdot\frac{d_o^3-d_i^3}{d_o^2-d_i^2}\cdots(1-1)$$
| $$d_w$$ | 等価摩擦直径 |
| $$d_o$$ | 座面の外側の直径 |
| $$d_i$$ | 座面の内側の直径 |

式は若干複雑ですが、覚える必要はないですよー。ちなみに、Diの値は、ねじのバカ穴径によって変わるので注意してください。
ではこれを使って摩擦力を表していきます。
今、ボルトに軸力Faが発生しているとします。
ボルト座面の滑り摩擦係数をμwとすると、最大静止摩擦力は以下のようになります。
$$f_w=\mu_w F_a$$
ここで、「締付けトルクに対して打ち勝てるか」を表現したいので、上式で表した最大静止摩擦力をトルク換算します。
このトルク換算した値が「座面で必要な締付けトルク」となります。
接触面全体における最大静止摩擦力は、等価摩擦直径で発生すると考えれば良いので、座面で必要な締付けトルクは以下のようになります。
$$\begin{align}
T_w&=\mu_w F_a \cdot\frac{d_w}{2}\cdots(1-2)
\end{align}$$
| $$T_w$$ | 座面で必要な締付けトルク |
| $$\mu_w$$ | 座面と母材との滑り摩擦係数 |
| $$F_a$$ | 軸力 |
| $$d_w$$ | 等価摩擦直径 |
以上が座面で発生する摩擦力です。

ねじ面で発生する摩擦力の話と比べると落差がすごいですが、本当にこれで終わりです(笑)
等価摩擦直径の値は覚える必要はないですが、それでも「大雑把でいいから、もうちょっと覚えやすい値はないのか?」と思う方もいらっしゃるかと思います。
そんな人のため、大雑把な値を言うと、六角ボルトで1.3d、六角穴付きボルトで1.3d~1.4dが目安となります(dはねじの呼び径)
以下に私で計算したいくつかのパターンを掲載しますが、先述の目安の値にほぼ同じ値になっていることがわかります。
| ねじの呼び d | 等価摩擦直径 | ||
|---|---|---|---|
| バカ穴1級 | バカ穴2級 | バカ穴3級 | |
| M3 | 3.93(1.31d) | 4.01(1.34d) | 4.10(1.37d) |
| M4 | 5.13(1.28d) | 5.22(1.31d) | 5.36(1.34d) |
| M5 | 6.12(1.22d) | 6.22(1.24d) | 6.36(1.27d) |
| M6 | 7.71(1.28d) | 7.80(1.30d) | 7.98(1.33d) |
| M8 | 10.10(1.26d) | 10.37(1.30d) | 10.84(1.35d) |
| M10 | 12.68(1.27d) | 12.90(1.29d) | 13.36(1.34d) |
| M12 | 18.17(1.24d) | 18.37(1.26d) | 18.78(1.30d) |
| M16 | 23.06(1.24d) | 23.26(1.26d) | 23.68(1.28d) |
| ねじの呼び d | 等価摩擦直径 | ||
|---|---|---|---|
| バカ穴1級 | バカ穴2級 | バカ穴3級 | |
| M3 | 4.45(1.48d) | 4.53(1.51d) | 4.62(1.54d) |
| M4 | 5.76(1.44d) | 5.84(1.46d) | 5.97(1.49d) |
| M5 | 7.02(1.40d) | 7.11(1.42d) | 7.23(1.45d) |
| M6 | 8.33(1.39d) | 8.42(1.40d) | 8.59(1.43d) |
| M8 | 10.86(1.36d) | 11.12(1.39d) | 11.57(1.45d) |
| M10 | 13.44(1.34d) | 13.65(1.37d) | 14.10(1.41d) |
| M12 | 15.63(1.30d) | 15.86(1.32d) | 16.31(1.36d) |
| M16 | 20.70(1.29d) | 20.92(1.31d) | 21.37(1.34d) |
等価摩擦直径は(1-1)式で表されるとだけ説明しましたが、「それじゃあ、納得できない!どうしても本当に正しいのか気になってしょうがない!」という人も中にはいるかと思いますので、ここではその証明をしていきます。
この証明は、積分さえ知っていれば、さほど難しくありません。
ねじを締め付けた際、ボルト(またはナット)と母材との接触面は、以下の図のようにドーナツ状になります。
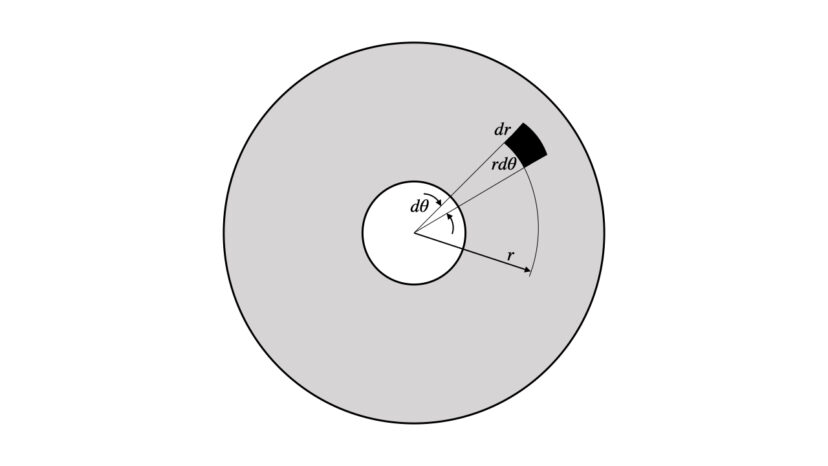
証明の流れとしては、この接触面のなかから、微小な要素を取出し、そこに発生する摩擦力について考えて、それを接触面積分だけ積分するといった感じです。
では始めていきます。
まず図のように、中心からrだけ離れた位置にある微小要素を取り出します。このとき、微小要素は「長方形」としてみなすと、微小要素の面積は以下の通りとなります。
$$a=dr\cdot rd\theta$$
| $$a$$ | 微小要素の面積 |
今、「単位面積あたりpの軸力」が発生しているとします。
よってねじを更に締め込むためには、この軸力によって発生する摩擦力に打ち勝つ必要があるということになります(ここではねじ面の摩擦力は考慮しません)。
まずは微小要素で発生する最大静止摩擦力を表すと、以下の通りとなります。
$$f_w’=\mu_w pa=\mu_w pdr\cdot rd\theta$$
| $$f_w’$$ | 微小要素における最大静止摩擦力 |
| $$\mu_w$$ | 座面と母材との滑り摩擦係数 |
| $$p$$ | 単位面積あたりの軸力 |
ただ、「締付けトルクに対して打ち勝てるか」を表現したいので、上式で表した最大静止摩擦力をトルク換算します。
これが要するに、微小要素あたりに必要な締付けトルクとなります。
$$\tau_w=f_w’\cdot r=\mu_w pdr\cdot rd\theta\cdot r$$
| $$\tau_w$$ | 微小要素あたりに必要な締付けトルク |
| $$f_w’$$ | 微小要素における最大静止摩擦力 |
| $$\mu_w$$ | 座面と母材との滑り摩擦係数 |
| $$p$$ | 単位面積あたりの軸力 |
これで、微小要素については表現できたので、これを座面の面積分だけ積分していきます。
$$\begin{align}
T_w&=\int_{r_i}^{r_o}\int_{0}^{2\pi}\tau_w\\
&=\int_{r_i}^{r_o}\int_{0}^{2\pi}\mu_w pdr\cdot rd\theta\cdot r\\
&=\mu_w p\int_{r_i}^{r_o}\int_{0}^{2\pi}r^2 d\theta dr\\
\end{align}$$
| $$T_w$$ | 座面で必要な締付けトルク |
| $$r_o$$ | 座面の外側の半径 |
| $$r_i$$ | 座面の内側の半径 |
| $$\tau_w$$ | 微小要素あたりに必要な締付けトルク |
| $$\mu_w$$ | 座面と母材との滑り摩擦係数 |
| $$p$$ | 単位面積あたりの軸力 |
二重積分で難しそうに見えますが、普通の定積分が2回分と考えればよいです。
まずはθから積分していきます。
$$\begin{align}
T_w&=\mu_w p\int_{r_i}^{r_o}\int_{0}^{2\pi}r^2 d\theta dr\\
&=\mu_w p\int_{r_i}^{r_o}r^2[\theta]_{0}^{2\pi} dr\\
&=\mu_w p\int_{r_i}^{r_o}2\pi r^2 dr
\end{align}$$
続いて、rの積分をしていきます。
$$\begin{align}
T_w&=\mu_w p\int_{r_i}^{r_o}2\pi r^2 dr\\
&=\mu_w p 2\pi [\frac{1}{3}r^3]_{r_i}^{r_o}\\
&=\mu_w p \frac{2}{3}\pi(r_o^3-r_i^3)\cdots(2-1)
\end{align}$$
ここからもうひと工夫します。
上の式の「p」は「単位面積あたりの軸力」であることから、「軸力を、接触面の面積で割った値」として表すことができます。
$$\begin{align}
p=\frac{F_a}{\pi(r_o^2-r_i^2)}\cdots(2-2)
\end{align}$$
| $$F_a$$ | 軸力 |
| $$r_o$$ | 座面の外側の半径 |
| $$r_i$$ | 座面の内側の半径 |
また、(2-1)(2-2)式について、riとroを、直径として表し直します。
$$\begin{cases}
T_w=\mu_w p \displaystyle\frac{2}{3}\cdot\displaystyle\frac{1}{8}\pi(d_o^3-d_i^3)\cdots(2-3)\\
p=\displaystyle\frac{4F_a}{\pi(d_o^2-d_i^2)}\cdots(2-4)
\end{cases}$$
ここまで来たら、(2-4)式を(2-3)式に代入します。
$$\begin{align}
T_w&=\mu_w \frac{4F_a}{\pi(d_o^2-d_i^2)} \frac{2}{3}\cdot\frac{1}{8}\pi(d_o^3-d_i^3)\\
&=\mu_w F_a \cdot\frac{1}{2}\frac{2}{3}\frac{d_o^3-d_i^3}{d_o^2-d_i^2}\cdots(2-5)
\end{align}$$
| $$d_o$$ | 座面の外側の直径 |
| $$d_i$$ | 座面の内側の直径 |
これが、ボルトを締め込む際に必要な、座面と母材との摩擦力に打ち勝つための締付けトルクになります。
この(2-5)式の右辺の一部をよく見ると、以下の等価摩擦直径の式の形をしていることがわかります。
$$d_w=\frac{2}{3}\cdot\frac{d_o^3-d_i^3}{d_o^2-d_i^2}$$
(2-5)式に、等価摩擦直径を導入すると以下のようになります。
$$\begin{align}
T_w&=\mu_w F_a \cdot\frac{1}{2}\frac{2}{3}\frac{d_o^3-d_i^3}{d_o^2-d_i^2}\\
&=\mu_w F_a \cdot\frac{d_w}{2}
\end{align}$$
以上が、等価摩擦直径の証明となります。
今回は座面で発生する摩擦力について解説していきました。
次回はねじの力学について、その他の知識・注意点について解説いたします。
今回は以上となります。ご一読ありがとうございました。
ねじ関連のおすすめ書籍▼
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

【解説】締め付けトルクと軸力の関係式の導出(2)
【解説】締め付けトルクと軸力の関係式の導出(4)