今回から、梁と曲げ荷重についてお話します。
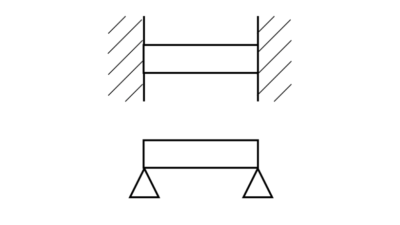
建物の骨組みを考えたときに、
地面に対して垂直に立っている材料のことを「柱」と言います。
これは、皆さんにも馴染みのある言葉だと思います。
しかし、柱だけでは建物の強度としては不十分です。
この柱同士を水平方向に繋いで、より強度の強い建物を作る必要があります。
この柱同士を繋ぐ部品のことを「梁(はり)」と言います。

建物を作る際はこの梁の上に、天井、床、屋根などを設置していきます。
この梁に関する知識や計算ですが、材料力学の中で、実際の設計で最も多用するものです。
そのため、この記事をご覧の皆さんには、是非ともマスターしていただきたいです。
ただ今回は、いきなり曲げ荷重や梁についての話ではなく、その前に知っておくべきこととして、導入的な内容をお話しします。
今までは、単なる「力」の問題について扱ってきましたが、ここからは力のモーメントに関する知識が必要となります。
中学校の教科書などでは「てこの原理」などと記載されているかもしれません。
力のモーメントは、
「回転中心からの距離×回転方向にかかる力」
で表されます。
少し復習をしてみましょう。
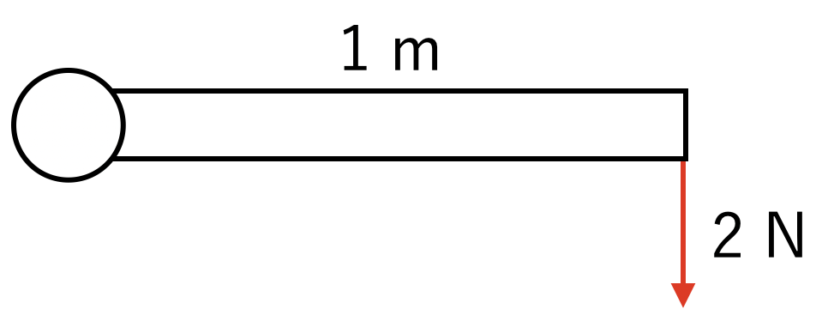
下の図においては、
回転方向にかかる力が2Nで、
回転中心からの距離が1mなので、
モーメントは2N×1m=2 N・mです。
一方、下の図においては、同じく回転中心からの距離が1mで、力は2Nです。
しかし、この力は回転方向を向いていないため、力のモーメントは0 N・mです。

また、同じ2Nの力でも、回転中心に対して力がかかっていれば、棒にかかるモーメントは0 N・mです。

簡単な話ではありますが、曲げ荷重の計算をするときは、これらの組み合わせを多用しますので、一度頭の中を整理しておくと良いと思います。
私が学生の頃「梁に対して短手方向に力がかかっていれば、曲げ荷重になる」と教わりました。
しかし、最初私は納得ができませんでした。
典型的な問題に、次のようなものがあります。
2つの台の上に梁が水平に固定されており、その中央で下向きの荷重がかかっています。
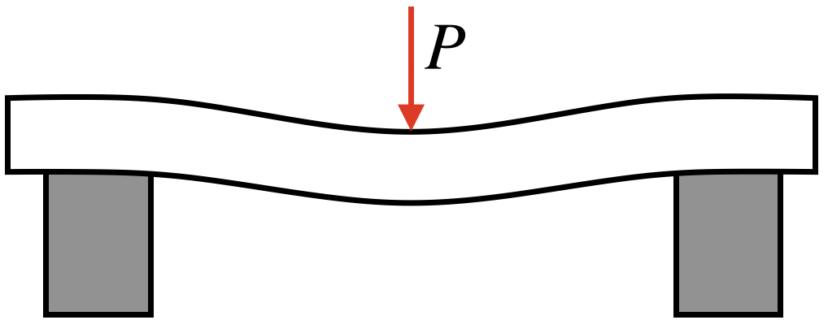
ただ、実際の梁が、人間の感覚でわかる程度に変形することはありません。
床がふにゃふにゃだったら、欠陥住宅です。
そのため、当初の私は、
「梁に対して短手方向の力」=「曲げ荷重』というのが、
イメージとして把握しづらかったのです。
悩んでいたある日、私は母親に頼まれて、家具をバラバラにすることになりました。
粗大ゴミで出すと高いから、燃えるゴミで出したかったそうです。
そんなに強固なものではなかったので、素手でバラバラにしていたのですが、
このバラバラにしていた時の作業そのものが曲げ荷重だったことに気づきました。
こんな感じです。

つまり、モノの端と端とを持って、膝で割っていました。
これで私の中で、曲げ荷重のイメージを定着させることができました。
もし、「梁」でイメージがわかない方がいれば、私のように身近なものに置き換えてみると良いと思います。
実際のものづくりの設計において、この曲げ荷重に関する計算が、群を抜いて多いです。
それは、私が床や屋根の設計をしているから、という訳ではありません(そもそも私は建屋の設計者ではないので・・・)
ものづくりには製品によって規模も用途も異なりますが、
実際に部品を使う状況を考えると、
ものづくり全般的に、曲げ荷重がかかるケースが多いのです。
例えば、皆さんの使っている机ですが、思いっきり肘をつくと若干沈み込みますよね。
これは、机の天板に曲げ荷重がかかっていると説明することができます。
また、数年前に
「iPhoneをズボンの後ろのポケットにいれたまま座ったりすると、iPhoneが曲がる」
などと世間で騒がれておりましたが、
これも曲げ荷重です。
曲げ荷重はモーメントですから、
たとえ小さな力であっても、中心軸から離れた位置に荷重をかければ、モーメントは増えます。
そのため、曲げ荷重による部品の破損には十分注意する必要があるのです。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


材料力学 演習問題 03【熱応力】
梁の支持方法と、使い分けの方法