球殻を引き離す力の解き方について教えて下さい。
今回は主に高校生向けにこのような問題の解き方について、お答えしていきます。
問題
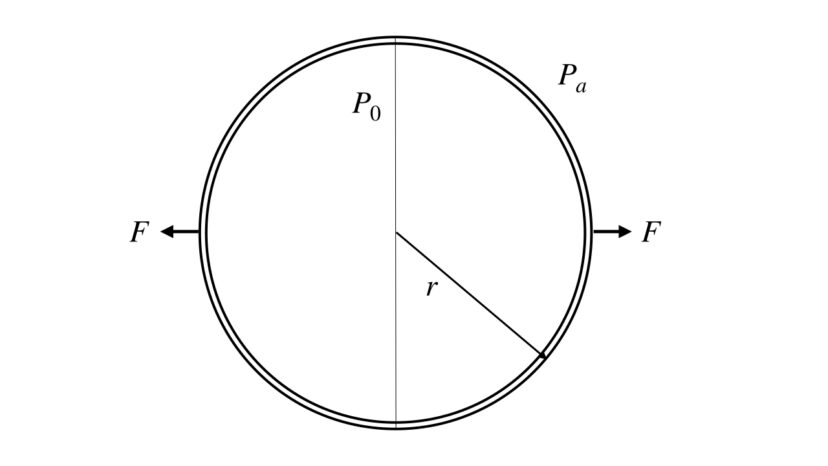
半径rの半球殻2個を合わせるようにくっつけて球殻を作ります。
その後、球殻内の圧力がP0になるまで真空引きをします。
図の位置・方向に半球殻を引っ張るとき、この半球殻を引き離すのに必要な力Fを求めてください。
ただし、大気圧はPaとし、球殻の厚さは十分に薄いとします。
半球殻のようなものを使って外部と内部とに空間を分けたあと、内部の気圧を大気圧よりも低くすると、半球殻がくっつきます。

吸盤がガラスやお風呂の壁にくっつく原理と一緒ですね。
今回はこの問題を2つの方法で解いていきたいと思います。
1つは正統派的に積分を使って求める、少し複雑な方法、
もう1つは、物理・数学のセンスがあれば解ける簡単な方法です。
ただ、少し複雑とは言いつつも、積分の練習には丁度いい問題となっております。
最近はコロナウイルスの影響で、あまり自宅から出れない状況が続いていますが、今回のような記事を高校物理の勉強に役立っていただければ幸いです。
積分を使って求める方法のロードマップは以下の通りとなります。
それでは順に解説をしていきます。
今回の問題では、微小領域を以下の図のようなドーナツ形状を設定します。
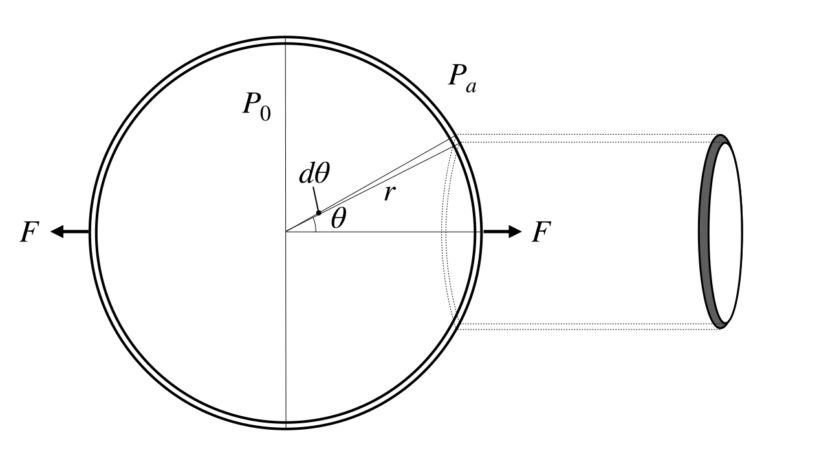
ここでは、2つのFを通るようにx軸を、x軸とのなす各をθ、微小角度をdθとします。
ドーナツの面積sの求め方ですが、
ドーナツの幅は、rdθ
ドーナツの円周は、半径rsinθの円周なので、2πrsinθ
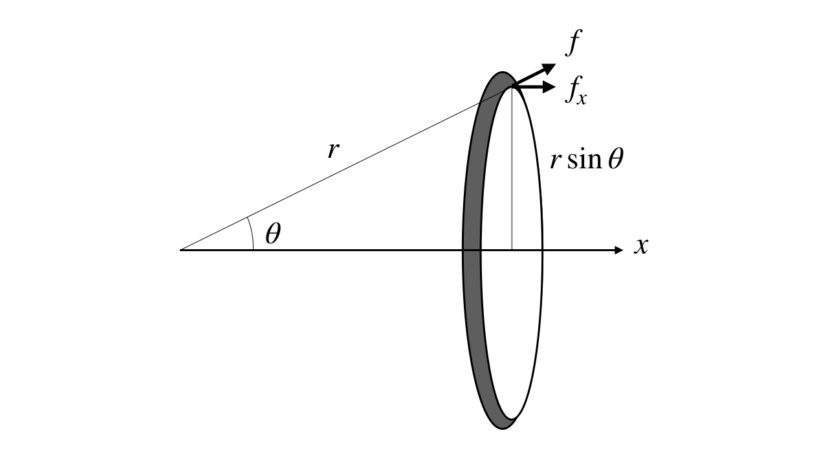
よって、ドーナツの面積sは
$$\begin{align}
s&=rd\theta 2\pi r\sin\theta\\
&=2\pi r^2\sin\theta d\theta
\end{align}$$
ドーナツが受ける力fは、圧力差に面積を掛けることで求められるので、
$$\begin{align}
f&=(P_a-P_0)s
\end{align}$$
となります。
(球殻の厚さは非常に薄いので、球殻の外側の表面積と、内側の表面積とは同じとみなして問題ありません)
このうち、x軸方向成分のみを取り出す必要があるので、cosθを掛けて
$$\begin{align}
f_x&=2(P_a-P_0)\pi r^2\sin\theta\cos\theta d\theta
\end{align}$$
となります。
先ほど求めたドーナツの面積を、半球殻の領域分足し合わせるために、積分を行います。
そのため積分区間は、θは0からπ/2までとなります。
また三角関数の部分は、倍角の公式を使って、積分ができる形状にしておきましょう。
$$\begin{align}
F&=\int_0^{\pi/2}f_x\\
&=(P_a-P_0)\pi r^2\int_0^{\pi/2}2\sin\theta\cos\theta d\theta\\
&=(P_a-P_0)\pi r^2\int_0^{\pi/2}\sin2\theta d\theta\\
&=(P_a-P_0)\pi r^2\left[\frac{-\cos2\theta}{2}\right]_0^{\pi/2}\\
&=(P_a-P_0)\pi r^2\frac{1+1}{2}\\
&=(P_a-P_0)\pi r^2
\end{align}$$
これが答えとなります。

倍角の公式は、三角関数の積分計算で多用するので、必ず覚えておきましょう。
$$\sin2\theta=2\sin\theta\cos\theta$$
$$\begin{align}
\cos2\theta&=\sin^2\theta-\cos^2\theta\\
&=2\sin^2\theta-1\\
&=1-2\cos^2\theta
\end{align}$$
先程は積分を使った正統派な方法を解説しましたが、
積分を使わなくても、簡単に計算することができますので解説します。
計算の前に、図を見てみましょう。
気圧が作用する面積ですが、
実は球殻の投影面積と等しくなります。
球殻の投影面積Sは、半球殻の分かれ目の断面積と同じなので
$$S=\pi r^2$$
となります。
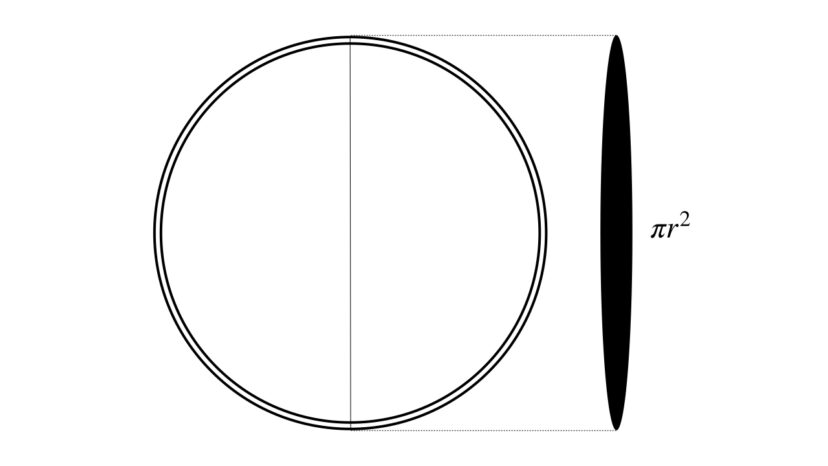
よって、半球殻を引き離す力Fは、
$$F=(P_a-P_0)\pi r^2$$
これが答えとなります。
この方法は、問題として与えられた状況をうまく分析するという物理・数学のセンスが必要にはなりますが、
計算量が少ないですし、面倒くさい積分の公式も不要です。
今回のポイントについてまとめると、以下の通りとなります。
余談ですが、実際に吸盤などを引き剥がす際には、
問題文のようにまっすぐ引っ張るよりも、
引き剥がす部分を少し潰したり、めくったりして、
空気が通る隙間を作ってあげるほうが、安全かつ簡単です。

ちょっとした裏技ですが、
定食に出てくる味噌汁は、フタを締めたままにしておくとフタが外れにくくなりますが、
お椀のふちのところを指で押すと、フタが外れやすくなります。
ただし、火傷に注意して、慎重に行ってください。
今回は以上となります。ご一読ありがとうございました。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

気泡の大きさの計算方法