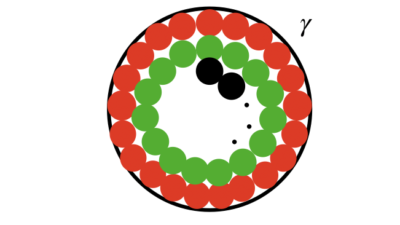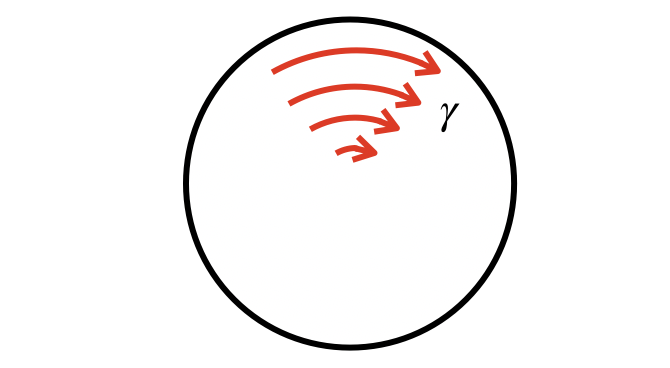
今回は、ねじり荷重におけるひずみについて、計算式を踏まえてお話をします。
ただし、いきなり計算式を眺めていても、材料に起っている現象が想像できないかたは、まずは以下の記事をご覧になることをお勧めします。
このねじり荷重のイメージを踏まえたうえで、
計算式としてどのように評価するかについて、今回お話していきます。
ただし ここでの話は、一様な丸棒が受けるねじり荷重という前提があることに 、注意してください。
トルク(ねじり荷重)は、円周方向にかかるせん断力です。
そして、回転中心から離れれば離れるほど、材料が受けるせん断力は大きくなります。
回転中心から離れるほど、材料が受けるせん断力が大きくなるということは、それに応じて、発生するひずみも大きくなります。
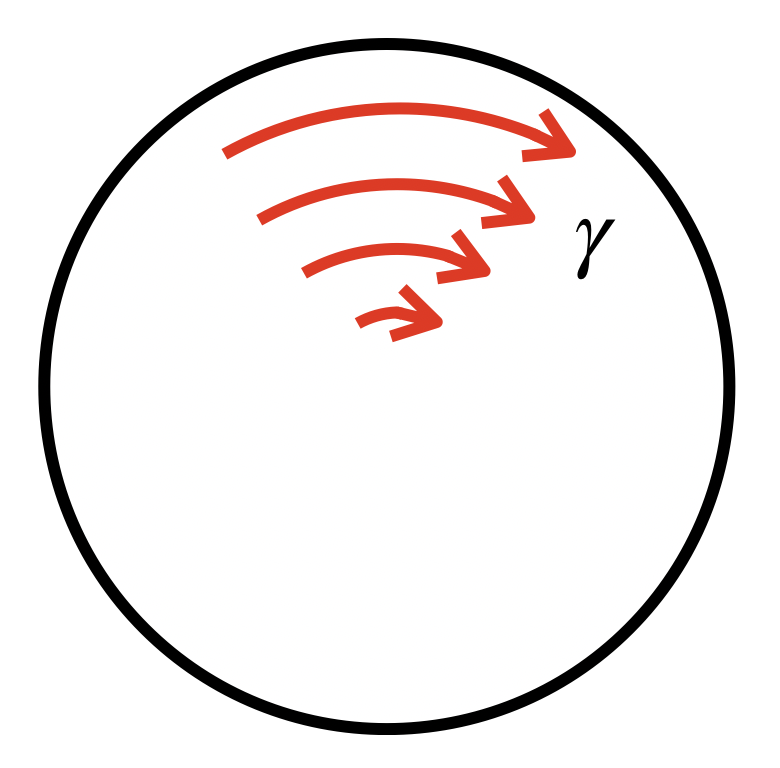
[mathjax]
$$\gamma=r\theta=r\frac{\phi}{L}$$
つまり、せん断ひずみγは、ねじりの中心からの距離rと、比ねじれ角θに比例します。
材料が弾性変形領域にあるとき、引張応力と引張ひずみとの関係は、以下の式で表すことができます。
$$\sigma=E\varepsilon$$
ここで、σ:引張応力、E:ヤング率(縦弾性係数)、ε:引張ひずみ です。
実は、せん断荷重やねじり荷重によって発生するせん断力にも、フックの法則が成り立ちます。それは以下の公式です。
$$\tau=G\gamma$$
ここで、τ:剪断応力、G:横弾性係数、γ:せん断ひずみ です。
引張応力のフックの法則も、せん断応力のフックの法則も、
応力とひずみの関係が、比例定数によって結ばれている点では、非常に似ている式です。
しかし、比例定数が異なることには注意が必要です。
横弾性係数もまた、ヤング率と同様に、材料の材質によって固有の値を持つ係数で、単位は[N/mm2]または[MPa]です。
例えばSS400と呼ばれる鉄鋼材料の場合、
ヤング率Eは、205,000 N/mm2 ですが、
横弾性係数Gは、81,000 N/mm2 です。
ねじり荷重によって発生する応力の計算は、曲げ荷重によって発生する応力の計算のときと同様で、単純には求めることができません。
なぜなら、ねじり荷重を受けている材料を仮想的に切り離したときに、底に発生する応力が一様ではないからです。
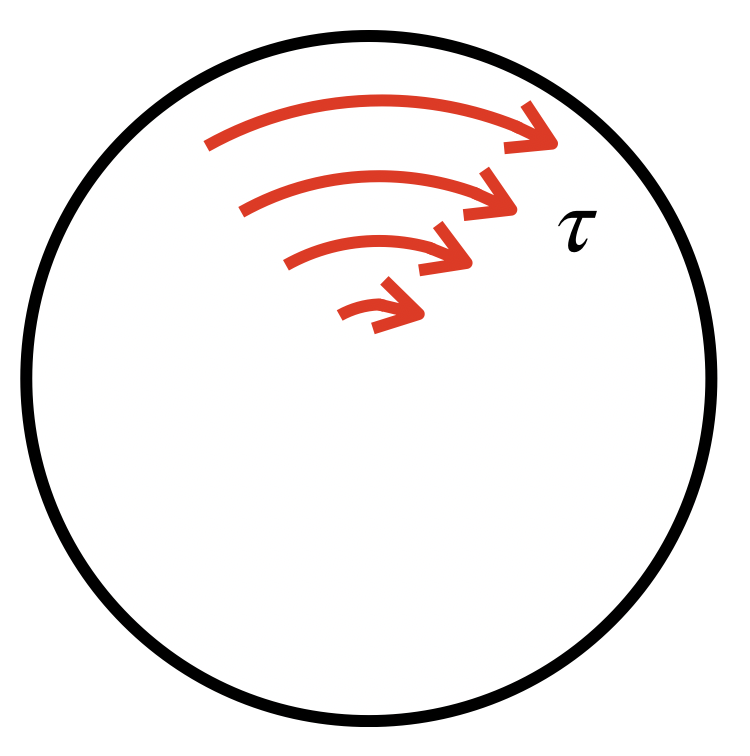
さらに、材料が一様な丸棒ではなかった場合、さらに複雑な計算が必要となります。
フックの法則で求めることができるせん断応力は、仮想断面上のある限られた領域に関するせん断応力です。
ねじり荷重の問題として求めるせん断応力は、これとは違い、
仮想断面上のあらゆるせん断応力について考慮することがあるので、注意が必要です。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

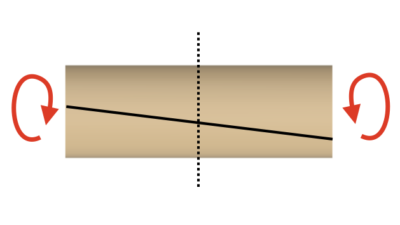
ねじりによる材料の変形は、角度で議論する
断面二次極モーメントの定義