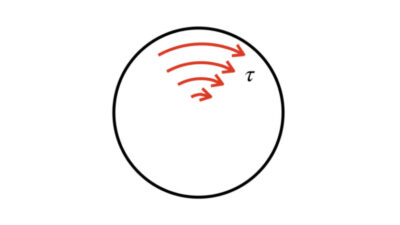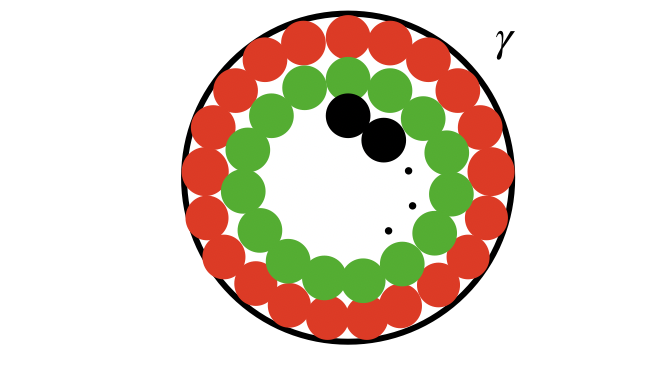
今回はねじれ応力の導出についてお話しします。
前回、ねじれ荷重におけるひずみの話をしました。
ここで登場したのは、以下の2つの式です。
$$\gamma=r\theta\cdots(1)\\
\tau=G\gamma\cdots(2)
$$
さらにねじりの応力の導出は、曲げ応力の導出方法と若干似ている部分があり、断面二次極モーメントという値を導入します。
そこで今回は、ねじりの応力を導出するために、これらの式と断面二次極モーメントについて、もう少し深掘りをしていきます。
例えば、中心からの距離をr、棒材の半径をaとすると、
ねじりによるせん断ひずみが最大になるのはr=aの位置です。
つまり、(1)式は以下のように書き換えることができます。
$$\gamma_{max}=a\theta\cdots(3)\\
$$
(1)式と(3)式とを合わせると、以下の関係式が得られます。
$$\gamma=\frac{r}{a}\gamma_{max}$$
さらに(2)式のフックの法則により、せん断応力についても同じような関係式が得られます。
$$
\frac{\tau}{G}=\frac{r}{a}\frac{\tau_{max}}{G}\\
\tau=\frac{r}{a}\tau_{max}\cdots(4)
$$
つまり、仮想断面上のある領域における応力やひずみは、
それぞれの最大値に、材料の半径に対する中心からの位置の比の掛け算としても求めることができます。
曲げ応力を求める際に行ったアプローチと同様に、応力の定義からねじり応力を求めていきます。
応力は「内力」を「仮想断面の面積」で割ったものです。
これは裏を返すと、「仮想断面上の応力を全て足すと、内力になる」と言うことです。
つまり、以下の図の赤や緑・黒の円の領域ひとつひとつにせん断応力がかかっています。
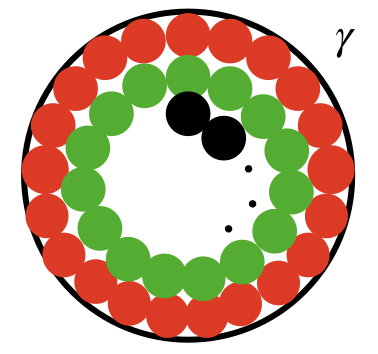
さらに、回転中心から見ると、これらの応力はモーメントとして作用します。
つまり、今回の場合において適用させると、応力と内力との関係として、以下の式が成り立ちます。
$$T=r_1\tau_1\times n_1+r_2\tau_2\times n_2+\cdots\quad \cdots(5)$$
(5)式は、先ほどの図の領域ひとつひとつが細分化されているほど、計算の精度が向上します。
ここで、(4)式を登場させることで、(5)式は以下のように簡略化させることができます。
$$T=\frac{\tau_{max}}{a}(r_1^2\times n_1+r_2^2\times n_2+\cdots)\quad \cdots(6)$$
さて、この右辺の()の中身が複雑であるので、曲げモーメントの導出の時と同様に、これを文字で置き換えます。
$$T=\frac{\tau_{max}}{a}I_p$$
このIpは断面二次極モーメントといい、材料の断面形状についてのねじり荷重のしにくさを表す値です。
単位は断面二次モーメントと同じく、[mm4]です。
先ほど、仮想断面状の領域が細分化されているほど、計算の精度が上がると言いましたが、計算の制御を向上させていくと、この断面二次極モーメントは、ある決まった値に近づいていくことがわかっております。
その値は、仮想断面の形状によって値がきまっており、例えば丸棒の場合は以下の式で求められます。
$$I_p=\frac{\pi d^4}{32}$$
ここでdは、丸棒の直径を表しております。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

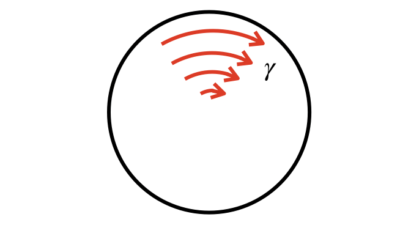
ねじり荷重におけるひずみとフックの法則
ねじりの応力の導出を解説