今回は、ねじり荷重における変形量についてお話しします。
ねじり荷重は、「材料の円周方向に働くせん断力」とも言い換えることができます。
せん断力は材料をずらすように変形させる力であり、その変形量は角度で表した通り、ねじり荷重においても、角度で変形量を議論します。
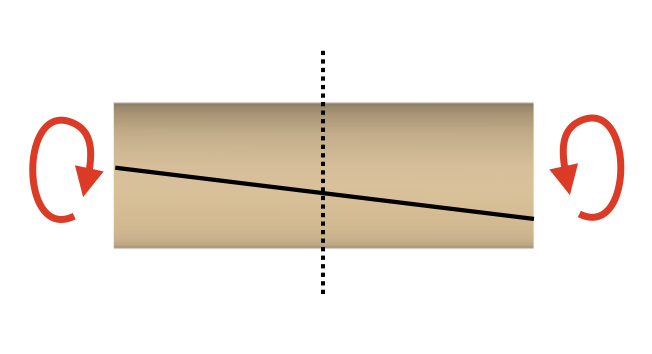
まず、ねじりが発生する範囲において、棒の表面に、棒の長手方向と平行になるような線を引きます。
そして、棒にトルクを加えると、先ほど棒に引いた線は、斜めになります。
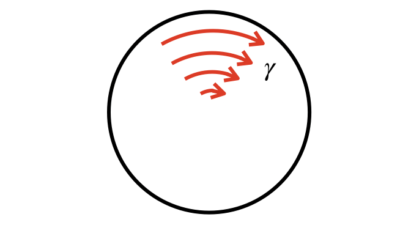
棒を断面から見てみると、荷重が加わる前と、荷重が加わった後とでは、ある角度分だけ回転します。

この角度が、ねじりによる材料の変形量に相当します。
この変形量のことを「ねじれ角」といい、記号Φで表します。
そんなねじり荷重の変形について、詳しくお話しします。
ねりじの変形量であるねじれ角ですが、これをそのまま材料の評価に適用することはできません。
ねじりの変形量を議論する上では、ねじれ角の代わりに比ねじれ角を使います。
その理由は、例えば材料を180度ねじる際にも、長さ100mmの軸と、長さ1000mmの軸とでは、ねじる容易さが異なるためです。
比ねじれ角という、単位長さあたりのねじれ角を使用することで、軸の長さの違いを無くしているのです。
比ねじれ角は、記号はθを使い、以下の式で表されます。
[mathjax]
$$
\theta=\frac{\phi}{L}
$$
材料にトルクを与えた場合、材料は長手方向に行くに従って断面が回転するように変形しますが、
断面の形状自体は変わらないという仮定を、材料力学ではします。
例えば、棒の断面に好きな模様やイラストを描いてねじっても、
その模様が歪んだりすることはありません。
ただし、断面形状が変わらないという仮定をするには一つ、前提条件があります。
それは、断面が円形でかつ軸方向に一様な場合のみ成り立つということです。
そのため、軸が四角形であったり、途中で径が変わるような段付きの軸の場合には適用することができません。
ねじり荷重における前提が成り立たない条件として、最も分かりやすいのは、雑巾しぼりの様子です。
雑巾を絞ると、雑巾の表面にはシワができます。

シンができるということは、材料が元の断面の形状を保てていない、つまり断面が歪んでいるということになります。
多くの材料力学の参考書を見ても、ねじりに関するページが比較的薄いのは、
ねじりが、この前提の上でしか議論ができないためと考えられます。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...


ねじり荷重とは
ねじり荷重におけるひずみとフックの法則