【解説】モータの計算式に出てくるナゾの係数の意味

2021年1月11日
設計
モータ, 計算, 設計

設計

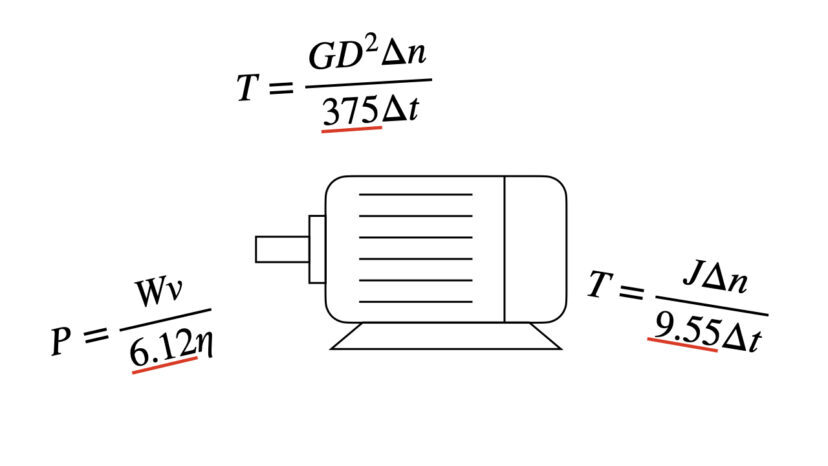
この記事を読むべき人

モータに関する計算をしているが、その計算式が正しい根拠がいまいちわからない人
モータの計算式に、わけのわからない係数があって気持ち悪いと感じている人/li>
モータの計算って、読む資料によって使っている式が違っており、わけがわからないと混乱している人

こんにちは、リヴィです。

私は普段、機械の設計をしています。

機械に使われるアクチュエータの中で、最もよく使われるのが「モータ」です。

モータって、小型の機械〜大型の機械まで幅広く使われます。コンベア、ロボットアーム、ポンプ、ブロワーなどはもちろんのこと、iPhoneの中にも、本体を振動させるための「振動モータ」や、カメラのピント調整をするためのモータなどが入っています。

そのため、設計にて能力計算をするときというのは、モータを選定するときが大半だったりします。

でも、モータの計算式を調べてみると、根拠のわからない係数がかかっていたりして、なかなか計算式の理解が困難だったりします。

この係数の根拠は、決して経験則からくる係数などではなく、

力の単位が「SI単位系」じゃなくて「重力単位系」だったり
「慣性モーメント」じゃなくて「GD²」だったり
回転数の単位が「rpm」だったり、「rad/s」だったり

といったように、実は単位変換が一つにまとめられているだけだったりします。

係数の意味がわからなくても、式に代入さえすれば計算できないことも無いです。ですが、式の意味を理解した上で使えるようになると、計算ミスや設計ミスをガクッと減少させることができます。

そこで今回は、モータの計算式に出てくる係数の意味について、詳しく解説していきます。

モータメーカの技術カタログを見ても詳しく書かれていないような内容ですので、この記事を読んで適切に計算ができるようにしていきましょう。

1 モータトルクの計算式
- 1.1 計算式その(1)
- 1.2 計算式その(2)
2 モータ容量の計算式
- 2.1 計算式その(1)
- 2.2 計算式その(2)
3 まとめ

モータトルクの計算式

計算式その(1)

$$T=\frac{J}{9.55}\frac{\Delta n}{\Delta t}=0.1047J\frac{\Delta n}{\Delta t}$$

$$T$$	トルク
$$J$$	慣性モーメント
$$n$$	回転数
$$t$$	時刻

モータトルクの計算式にはよく「1/9.55」または「0.1047」という係数が出てきます。

これは、「rpm」を「rad/s」へ変換するための係数です。

$$\begin{align}T [N･m]&=\frac{J [kg･m^2]}{9.55}\frac{\Delta n [rpm]}{\Delta t [s]}=0.1047J [kg･m^2]\frac{\Delta n [rpm]}{\Delta t [s]}\\&=J [kg･m^2]\frac{\Delta n [rpm]}{\Delta t [s]}\frac{2\pi}{60}\\&=J [kg･m^2]\frac{\Delta \omega [rad/s]}{\Delta t [s]}\end{align}$$

$$T$$	トルク
$$J$$	慣性モーメント
$$n$$	回転数
$$\omega$$	角速度
$$t$$	時刻

SI単位系的には「rad/s」だし、「rad/s」の方が余計な係数が計算式に出てきません。

ですが、モータのスペックシートなどでは「rpm」が使われていることがほとんどです。

よって、「rpm」の数値をそのまま代入できるようにするために上記のような計算式になっています。

ちなみに、「rpm」とは「revolutions per minute」、つまり「1分間あたりの回転」という意味です。

「1回転」をラジアンで表すと「2π」ですし、「1分」を秒で表すと「60秒」です。

そのためrpmをrad/sに変換するのに「2π/60」をかける必要があります。

ポイント

$$\omega[rad/s]=\frac{2\pi}{60}n[rpm]$$

日本人にとって「ラジアン」という単位はあまりなじみがないですよねー。「度」とか「回転」の方が多用されます。

計算式その(2)

$$T=\frac{GD^2}{375}\frac{\Delta n}{\Delta t}$$

$$T$$	トルク
$$GD^2$$	GD²
$$n$$	回転数
$$t$$	時刻

こちらは、少し古い計算資料に使われている式です。

この「1/375」という数字には、

「rpm」から「rad/s」への変換
「kgf」から「N」への変換
「GD²」から「慣性モーメント」

の3つの変換に使われる数字がごっちゃ混ぜになっています。

この「1/375」をわかりやすくなるように分解していくと、以下のようになります。

$$\begin{align}T[kgf･m]&=\frac{GD^2[kgf･m^2]}{375}\frac{\Delta n[rpm]}{\Delta t[s]}\\T[kgf･m]\cdot 9.8&=\frac{GD^2[kgf･m^2]}{4}\frac{\Delta n[rpm]}{\Delta t[s]}\frac{2\pi}{60}\\T[N･m]&=J[kg･m^2]\frac{\Delta \omega[rad/s]}{\Delta t[s]}\end{align}$$

$$T$$	トルク
$$GD^2$$	GD²
$$J$$	慣性モーメント
$$n$$	回転数
$$\omega$$	角速度
$$t$$	時刻

ポイント

$$T[N･m]=T[kgf･m]\cdot9.8$$

$$J[kg･m^2]=\frac{GD^2[kgf･m^2]}{4}$$

「1/375」の式が昔の計算資料だと出てくる理由は、昔は重力単位系で計算するのが普通だったからです。

それが今のようにSI単位系が使われるようになったのは平成11年からなので、割と最近の話です。

大企業に就職すると、年配の方などはまだまだ重力単位系を使って計算していたりします。使う必要はありませんが、理解はできるようにしておいたほうがいいですねー

ちなみに、GD²は「ジー・ディー・スクエア（スケア）」と呼びます。

ググると「はずみ車効果」とか「フライホイール効果」とかと出てきますが、そのように呼ぶ人はほとんどいません。

モータ容量の計算式

計算式その(1)

$$P=\frac{Tn}{9549}=0.1047Tn$$

$$P$$	容量
$$T$$	トルク
$$n$$	回転数

この「1/9549」は、容量が割と大きめのモータの計算書に掲載されております。

その理由は、容量Pの単位が「kW」だからです。

プラント設備向けや、クレーン用のモータなどでよく目にする係数ですね！

この係数の意味がわかるように式を変換していくと、以下の通りとなります。

$$\begin{align}P[kW]&=\frac{T[N･m]\cdot n[rpm]}{9549}\\&=T[N･m]\cdot n[rpm]\frac{2\pi}{60}\cdot10^{-3}\\&=T[N･m]\cdot\omega[rad/s]\cdot10^{-3}\end{align}$$