材料力学の解き方として、初歩的な問題、たとえば材料に発生する内力が、材料の位置によらず一定である場合は、材料を仮想的に切り離す方法で問題を解くと簡単です。
しかし、少し複雑な問題、たとえば内力が材料の位置によって連続的に変化するような問題では、材料を仮想的に切り離す方法で解くのは、かなり難しいです。
このような問題の場合、材料を微小要素に切り分けて解く方法で解くのが得策です。
そのような解き方の練習として、以下のような問題を取り上げながら、微小要素に切り分けて解く方法についてお話ししていきます。
【問題】
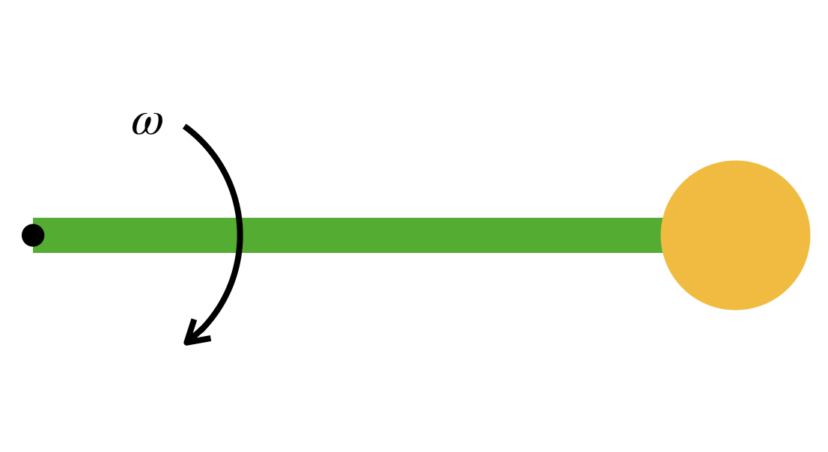
直径D、長さL、密度ρの一様な丸棒の片端に、質量Mの重りを固定し、もう一方の片端を回転ができるように固定します。この棒を一定の角速度ωで円運動させたときの棒の伸びはいくらになるかを計算してください。ただし、ヤング率をE、材料の変形はフックの法則が成立する範囲、重力加速度は無視することとします。

全体の力の関係について考えます。
まず、棒自体が回転しているため、遠心力(慣性力)を受けます。
ここではF aとします。
さらに、棒の端がおもりと固定されておりますので、おもりから力を受けます。ここではFbとします。
よって、力の関係は、以下のようになります。
解く方針についてですが、「棒の伸び(変形量)」を求めるためには、「ひずみ」を求める必要があります。
「ひずみ」を求める際には、フックの法則を使って、「応力」と「ヤング率」から求めることができます。
ヤング率は問題で与えられておりますので、求める必要があるのは「応力」です。
「応力」は棒が受ける「荷重」と「断面積」から求めることができますが、「断面積」は一定なので、「荷重」を求める必要があります。
この荷重は上記の図に示したとおり、「棒自身が受ける遠心力」と「おもりから受ける作用力」とに分けることができます。
棒自身が受ける遠心力を求めていきますが、棒が受ける遠心力は、旋回中心からの位置によって値が異なります。
そのため、棒を微小要素に切り分けて考えて行くこととします。
棒の旋回中心をr=0としたとき、r=rと、r=r+drとの間に挟まれた微小要素について、まずこの微小要素の質量は以下のように表されます。
$$\begin{align}
&((r+dr)-r)\cdot\frac{\pi D^2}{4}\cdot\rho\\
&=\frac{\pi d^2\rho}{4}dr
\end{align}$$
ポイント
(質量)=(体積)×(密度)
よって、この微小要素が受ける遠心力は以下のようになります。
$$f=\frac{\pi D^2\rho}{4}dr\cdot r \cdot \omega^2$$
ポイント
(遠心力)
=(質量)×(回転半径)×(角速度)2
棒全体の遠心力は、棒の中心側の端の位置から、外側の端の位置まで積分をすれば良いので、
$$\begin{align}
F_a&=\int^L_0\frac{\pi D^2\rho}{4}\cdot r \cdot \omega^2 dr\\
&=\frac{\pi D^2\rho\omega^2}{4}\int^L_0 r dr\\
&=\frac{\pi D^2\rho\omega^2}{4}[\frac{1}{2}r^2]^L_0\\
&=\frac{\pi D^2\rho\omega^2L^2}{8}
\end{align}$$
まずは棒の外力に相当する「おもりの遠心力」を求めていきます。
重りが受ける遠心力をFgとすると、以下のようになります。
$$F_g=ML\omega^2$$
この力が、棒から受ける反作用力と釣り合うので、
$$F_b=F_g=ML\omega^2
以上により、棒が受ける力は次のようになります。
$$\begin{align}
F&=F_a+F_b\\
&=\frac{\pi D^2\rho\omega^2L^2}{8}+ML\omega^2
\end{align}$$
よって、「ひずみと変形量との関係」「フックの法則」「力と応力の関係」を使用することで、棒の伸びΔLは以下のように表すことができます。
$$\begin{align}
\Delta L&=\varepsilon L\\
&=\frac{\sigma}{E}L\\
&=\frac{4F}{\pi D^2 E}L\\
&=(\frac{\pi D^2\rho\omega^2L^2}{8}+ML\omega^2) \frac{4L}{\pi D^2 E}\\
&=\frac{\omega^2}{E}(\frac{\rho L^3}{2}+\frac{4ML^2}{\pi D^2})
\end{align}$$
これが解答となります。
ものづくりのススメでは、機械設計の業務委託も承っております。
ご相談は無料ですので、以下のリンクからお気軽にお問い合わせください。

機械設計の無料見積もり
機械設計のご依頼も承っております。こちらからお気軽にご相談ください。
構想設計 / 基本設計 / 詳細設計 / 3Dモデル / 図面 / etc...

引張荷重による材料の変形量を微小要素に分けて求める方法【材料力学】
2つの平板間の熱応力の計算方法